Подмножество
После того как введено понятие множества, возникает задача конструирования новых множеств из уже имеющихся, то есть определить операции над множествами.
Множество М', каждый элемент, которого является элементом другого множества М, называется подмножеством данного множества М. Таким образом, множество М' называется подмножеством множества М тогда и только тогда, когда любой элемент множества М' принадлежит множеству М:
Любое множество  является своим подмножеством. Если мы хотим исключить
является своим подмножеством. Если мы хотим исключить  из рассмотрения, мы пользуемся понятиемсо́бственного подмножества, которое определяется так:
из рассмотрения, мы пользуемся понятиемсо́бственного подмножества, которое определяется так:
Множество  является собственным подмножеством множества
является собственным подмножеством множества  , если
, если 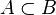 и
и 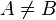 .
.
Пустое множество является подмножеством любого множества. Если мы вдобавок хотим исключить из рассмотрения пустое множество, мы пользуемся понятием нетривиа́льного подмножества, которое определяется так:
Множество  является нетривиальным подмножеством множества
является нетривиальным подмножеством множества  , если
, если  является собственным подмножеством
является собственным подмножеством  и
и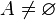 .
.
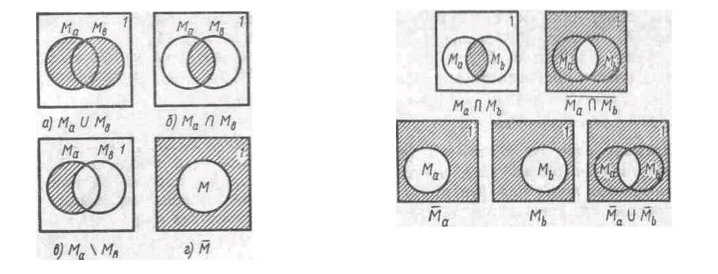
Операции объединения пересечения, разности и дополнения проиллюстрированы.

Минимизации представления множества

Строгий или нестрогий порядок, заданный на полностью упорядоченном множестве <X, R>, называется линейным порядком.
Пример 1. Все множества чисел линейно упорядочены, так как для любых чисел из этих множеств одно меньше другого или они равны.

