1. Консервативные и неконсервативные силы. Сила упругости как консервативная сила.
Сила называется консервативной или потенциальной, если ее работа A не зависит от траектории, а определяется только начальным и конечным положениями тела. Работа таких сил по перемещению тела по замкнутой траектории всегда равна нулю.
Примеры: сила тяжести, сила упругости, гравитационная сила.
Гравитационная сила, сила упругости, кулоновская сила электростатического взаимодействия относятся к так называемым центральным силам.
Центральными называются силы, направленные к одной и той же точке (либо от неё). Эта точка называется силовым центром. Величина центральной силы зависит только от расстояния до силового центра r
Для удобства расчета работы таких сил вводится понятие потенциальной энергии Wп:
A=Wп1−Wп2.
Работа разных сил при перемещении одного и того же тела различна. Заметим, что перемещение может зависеть от выбора системы отсчета, следовательно, работа в разных системах отсчета также может отличаться.
Если работа силы зависит от траектории, то такие силы называются неконсервативными. Как правило, эти силы зависят от вектора скорости (от его модуля или направления). Работа таких сил может приводить к выделению тепла (диссипации энергии). Неконсервативными являются силы трения и сопротивления.
Вычислим, например, работу, которую совершает сила тяжести при переходах частицы разными путями из положения 1 в положение 2 . Если этот переход произошёл по вертикали, то работа силы :
.
Теперь пусть та же частица переместится из 1 в 2 по пути 1-1’-2. Здесь промежуточная точка 1’ находится на высоте h2.
Полная работа будет складываться из работ силы тяжести на участках 1-1’ и 1’-2:
.
Работа силы тяжести на горизонтальном участке 1’-2 равна нулю, так как здесь вектор силы нормален перемещению. Мы вновь получили прежний результат, свидетельствующий о том, что работа силы тяжести не зависит от формы траектории. Этот вывод легко обобщается и на случай произвольной криволинейной траектории, соединяющей начальную и конечную точки пути.
2. Работа сил электростатического поля при перемещении заряда. Циркуляции вектора напряжённости. Потенциальный характер электростатического поля.
Работа в электрическом поле. Потенциал
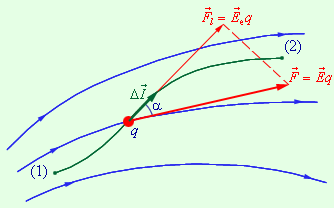
При перемещении пробного заряда q в электрическом поле электрические силы совершают работу. Эта работа при малом перемещении 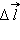 равна (рис. 1.4.1):
равна (рис. 1.4.1):
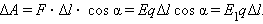 |
|
|
| Рисунок 1.4.1.
Работа электрических сил при малом перемещении
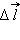 заряда q заряда q |
Рассмотрим работу сил в электрическом поле, создаваемом неизменным во времени распределенным зарядом, т.е. электростатическом поле
Электростатическое поле обладает важным свойством:
Работа сил электростатического поля при перемещении заряда из одной точки поля в другую не зависит от формы траектории, а определяется только положением начальной и конечной точек и величиной заряда.
Аналогичным свойством обладает и гравитационное поле, и в этом нет ничего удивительного, так как гравитационные и кулоновские силы описываются одинаковыми соотношениями.
Следствием независимости работы от формы траектории является следующее утверждение:
Работа сил электростатического поля при перемещении заряда по любой замкнутой траектории равна нулю.
Силовые поля, обладающие этим свойством, называют потенциальными или консервативными.
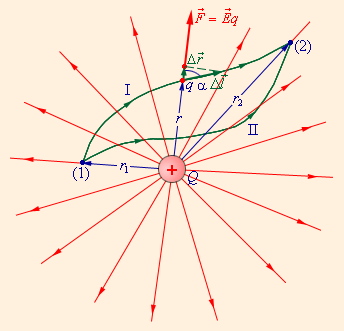
На рис. 1.4.2 изображены силовые линии кулоновского поля точечного заряда Q и две различные траектории перемещения пробного заряда q из начальной точки (1) в конечную точку (2). На одной из траекторий выделено малое перемещение 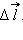 Работа ΔA кулоновских сил на этом перемещении равна
Работа ΔA кулоновских сил на этом перемещении равна
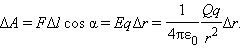 |
Таким образом, работа на малом перемещении зависит только от расстояния r между зарядами и его изменения Δr. Если это выражение проинтегрировать на интервале от r = r1 до r = r2, то можно получить
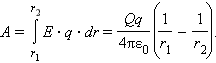 |
|
|
| Рисунок 1.4.2.
Работа кулоновских сил при перемещении заряда q зависит только от расстояний r1 и r2 начальной и конечной точек траектории
|
Полученный результат не зависит от формы траектории. На траекториях I и II, изображенных на рис. 1.4.2, работы кулоновских сил одинаковы. Если на одной из траекторий изменить направление перемещения заряда q на противоположное, то работа изменит знак. Отсюда следует, что на замкнутой траектории работа кулоновских сил равна нулю.
Если электростатическое поле создается совокупностью точечных зарядов 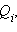 то при перемещении пробного заряда q работа A результирующего поля в соответствии с принципом суперпозиции будет складываться из работ
то при перемещении пробного заряда q работа A результирующего поля в соответствии с принципом суперпозиции будет складываться из работ 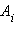 кулоновских полей точечных зарядов:
кулоновских полей точечных зарядов: 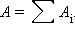 Так как каждый член суммы
Так как каждый член суммы 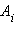 не зависит от формы траектории, то и полная работа A результирующего поля не зависит от пути и определяется только положением начальной и конечной точек.
не зависит от формы траектории, то и полная работа A результирующего поля не зависит от пути и определяется только положением начальной и конечной точек.
Свойство потенциальности электростатического поля позволяет ввести понятие потенциальной энергии заряда в электрическом поле. Для этого в пространстве выбирается некоторая точка (0), и потенциальная энергия заряда q, помещенного в эту точку, принимается равной нулю.
Потенциальная энергия заряда q, помещенного в любую точку (1) пространства, относительно фиксированной точки (0) равна работе A10, которую совершит электростатическое поле при перемещении заряда q из точки (1) в точку (0):
|
(В электростатике энергию принято обозначать буквой W, так как буквой E обозначают напряженность поля.)
Так же, как и в механике, потенциальная энергия определена с точностью до постоянной величины, зависящей от выбора опорной точки (0). Такая неоднозначность в определении потенциальной энергии не приводит к каким-либо недоразумениям, так как физический смысл имеет не сама потенциальная энергия, а разность ее значений в двух точках пространства.
Работа, совершаемая электростатическое полем при перемещении точечного заряда q из точки (1) в точку (2), равна разности значений потенциальной энергии в этих точках и не зависит от пути перемещения заряда и от выбора точки (0).
|
Потенциальная энергия заряда q, помещенного в электростатическое поле, пропорциональна величине этого заряда.
Физическую величину, равную отношению потенциальной энергии электрического заряда в электростатическом поле к величине этого заряда, называют потенциалом φ электрического поля:
|
Потенциал φ является энергетической характеристикой электростатического поля.
Работа A12 по перемещению электрического заряда q из начальной точки (1) в конечную точку (2) равна произведению заряда на разность потенциалов (φ1 – φ2) начальной и конечной точек:
| A12 = Wp1 – Wp2 = qφ1 – qφ2 = q(φ1 – φ2). |
В Международной системе единиц (СИ) единицей потенциала является вольт (В).
| 1 В = 1 Дж / 1 Кл. |
Во многих задачах электростатики при вычислении потенциалов за опорную точку (0) удобно принять бесконечно удаленную точку. В этом случае понятие потенциала может быть определено следующим образом:
Потенциал поля в данной точке пространства равен работе, которую совершают электрические силы при удалении единичного положительного заряда из данной точки в бесконечность.
|
Потенциал φ∞ поля точечного заряда Q на расстоянии r от него относительно бесконечно удаленной точки вычисляется следующим образом:
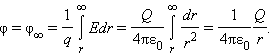 |
Как следует из теоремы Гаусса, эта же формула выражает потенциал поля однородно заряженного шара (или сферы) при r ≥ R, где R – радиус шара.
Для наглядного представления электростатическое поля наряду с силовыми линиями используют эквипотенциальные поверхности.
Поверхность, во всех точках которой потенциал электрического поля имеет одинаковые значения, называется эквипотенциальной поверхностью или поверхностью равного потенциала.
Силовые линии электростатическое поля всегда перпендикулярны эквипотенциальным поверхностям.
Эквипотенциальные поверхности кулоновского поля точечного заряда – концентрические сферы. На рис. 1.4.3 представлены картины силовых линий и эквипотенциальных поверхностей некоторых простых электростатических полей.
|
|
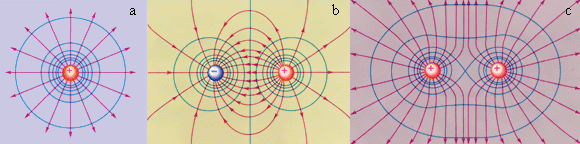
| Рисунок 1.4.3.
Эквипотенциальные поверхности (синие линии) и силовые линии (красные линии) простых электрических полей: a – точечный заряд; b – электрический диполь; c – два равных положительных заряда
|
В случае однородного поля эквипотенциальные поверхности представляют собой систему параллельных плоскостей.
Если пробный заряд q совершил малое перемещение 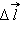 вдоль силовой линии из точки (1) в точку (2), то можно записать:
вдоль силовой линии из точки (1) в точку (2), то можно записать:
| ΔA12 = qEΔl = q(φ1 – φ2) = – qΔφ, |
где Δφ = φ1 – φ2 – изменение потенциала. Отсюда следует
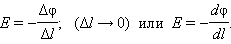 |
Это соотношение в скалярной форме выражает связь между напряженностью поля и потенциалом. Здесь l – координата, отсчитываемая вдоль силовой линии.
Из принципа суперпозиции напряженностей полей, создаваемых электрическими зарядами, следует принцип суперпозиции для потенциалов:
| φ = φ1 + φ2 + φ3 + ... |
Циркуляцией вектора напряженности называется работа, которую совершают электрические силы при перемещении единичного положительного заряда по замкнутому пути L
 |
(13.18) |
Так как работа сил электростатического поля по замкнутому контуру равна нулю (работа сил потенциального поля), следовательно циркуляция напряженности электростатического поля по замкнутому контуру равна нулю.

3. Теорема о циркуляции для вектора магнитной индукции (закон постоянного тока). Теорема Гаусса для вектора В
Закон Био–Савара. Теорема о циркуляции
Магнитное поле постоянных токов различной конфигурации изучалось экспериментально французскими учеными Ж. Био и Ф. Саваром (1820 г.). Они пришли к выводу, что индукция магнитного поля токов, текущих по проводнику, определяется совместным действием всех отдельных участков проводника. Магнитное поле подчиняется принципу суперпозиции:
Если магнитное поле создается несколькими проводниками с током, то индукция результирующего поля есть векторная сумма индукций полей, создаваемых каждым проводником в отдельности.
Индукцию 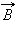 проводника с током можно представить как векторную сумму элементарных индукций
проводника с током можно представить как векторную сумму элементарных индукций 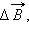 создаваемых отдельными участками проводника. На опыте невозможно выделить отдельный участок проводника с током, так как постоянные токи всегда замкнуты. Можно измерить только суммарную индукцию магнитного поля, создаваемого всеми элементами тока. Закон Био–Савара определяет вклад
создаваемых отдельными участками проводника. На опыте невозможно выделить отдельный участок проводника с током, так как постоянные токи всегда замкнуты. Можно измерить только суммарную индукцию магнитного поля, создаваемого всеми элементами тока. Закон Био–Савара определяет вклад 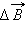 в магнитную индукцию
в магнитную индукцию 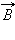 результирующего магнитного поля, создаваемый малым участком Δl проводника с током I.
результирующего магнитного поля, создаваемый малым участком Δl проводника с током I.
|
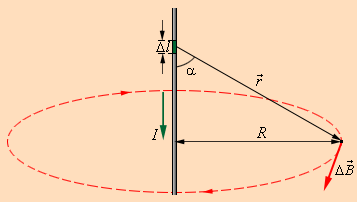
Здесь r – расстояние от данного участка Δl до точки наблюдения, α – угол между направлением на точку наблюдения и направлением тока на данном участке, μ0 – магнитная постоянная. Направление вектора 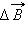 определяется правилом буравчика: оно совпадает с направлением вращения рукоятки буравчика при его поступательном перемещении вдоль тока. Рис. 1.17.1 иллюстрирует закон Био–Савара на примере магнитного поля прямолинейного проводника с током. Если просуммировать (проинтегрировать) вклады в магнитное поле всех отдельных участков прямолинейного проводника с током, то получится формула для магнитной индукции поля прямого тока:
определяется правилом буравчика: оно совпадает с направлением вращения рукоятки буравчика при его поступательном перемещении вдоль тока. Рис. 1.17.1 иллюстрирует закон Био–Савара на примере магнитного поля прямолинейного проводника с током. Если просуммировать (проинтегрировать) вклады в магнитное поле всех отдельных участков прямолинейного проводника с током, то получится формула для магнитной индукции поля прямого тока:
|
которая уже приводилась в § 1.16.
|
|
| Рисунок 1.17.1.
Иллюстрация закона Био–Савара
|
Закон Био–Савара позволяет рассчитывать магнитные поля токов различных конфигураций. Нетрудно, например, выполнить расчет магнитного поля в центре кругового витка с током. Этот расчет приводит к формуле
|
где R – радиус кругового проводника. Для определения направления вектора 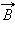 также можно использовать правило буравчика, только теперь его рукоятку нужно вращать в направлении кругового тока, а поступательное перемещение буравчика укажет направление вектора магнитной индукции.
также можно использовать правило буравчика, только теперь его рукоятку нужно вращать в направлении кругового тока, а поступательное перемещение буравчика укажет направление вектора магнитной индукции.
Расчеты магнитного поля часто упрощаются при учете симметрии в конфигурации токов, создающих поле. В этом случае можно пользаоваться теоремой о циркуляции вектора магнитной индукции, которая в теории магнитного поля токов играет ту же роль, что и теорема Гаусса в электростатике.
Поясним понятие циркуляции вектора 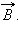 Пусть в пространстве, где создано магнитное поле, выбран некоторый условный замкнутый контур (не обязательно плоский) и указано положительное направление его обхода. На каждом отдельном малом участке Δl этого контура можно определить касательную составляющую
Пусть в пространстве, где создано магнитное поле, выбран некоторый условный замкнутый контур (не обязательно плоский) и указано положительное направление его обхода. На каждом отдельном малом участке Δl этого контура можно определить касательную составляющую 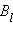 вектора
вектора 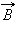 в данном месте, то есть определить проекцию вектора
в данном месте, то есть определить проекцию вектора 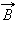 на направление касательной к данному участку контура (рис. 1.17.2).
на направление касательной к данному участку контура (рис. 1.17.2).
|
|
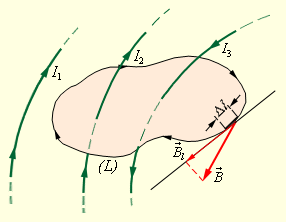
| Рисунок 1.17.2.
Замкнутый контур (L) с заданным направлением обхода. Изображены токи I1, I2 и I3, создающие магнитное поле
|
Циркуляцией вектора 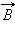 называют сумму произведений
называют сумму произведений 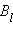 Δl, взятую по всему контуру L:
Δl, взятую по всему контуру L:
 |
Некоторые токи, создающие магнитное поле, могут пронизывать выбранный контур L в то время, как другие токи могут находиться в стороне от контура.
Теорема о циркуляции утверждает, что циркуляция вектора 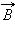 магнитного поля постоянных токов по любому контуру L всегда равна произведению магнитной постоянной μ0на сумму всех токов, пронизывающих контур:
магнитного поля постоянных токов по любому контуру L всегда равна произведению магнитной постоянной μ0на сумму всех токов, пронизывающих контур:
|
В качестве примера на рис. 1.17.2 изображены несколько проводников с токами, создающими магнитное поле. Токи I2 и I3 пронизывают контур L в противоположных направлениях, им должны быть приписаны разные знаки – положительными считаются токи, которые связаны с выбранным направлением обхода контура правилом правого винта (буравчика). Следовательно, I3 > 0, а I2 < 0. Ток I1 не пронизывает контур L.
Теорема о циркуляции в данном примере выражается соотношением:
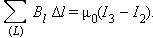 |
Теорема о циркуляции в общем виде следует из закона Био–Савара и принципа суперпозиции.
Простейшим примером применения теоремы о циркуляции является вывод формулы для магнитной индукции поля прямолинейного проводника с током. Учитывая симметрию в данной задаче, контур L целесообразно выбрать в виде окружности некоторого радиуса R, лежащей в перпендикулярной проводнику плоскости. Центр окружности находится в некоторой точке проводника. В силу симметрии вектор 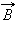 направлен по касательной
направлен по касательной 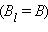 , а его модуль одинаков во всех точках окружности. Применение теоремы о циркуляции приводит к соотношению:
, а его модуль одинаков во всех точках окружности. Применение теоремы о циркуляции приводит к соотношению:
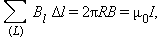 |
откуда следует формула для модуля магнитной индукции поля прямолинейного проводника с током, приведенная ранее.
Этот пример показывает, что теорема о циркуляции вектора магнитной индукции 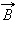 может быть использована для расчета магнитных полей, создаваемых симметричным распределением токов, когда из соображений симметрии можно «угадать» общую структуру поля.
может быть использована для расчета магнитных полей, создаваемых симметричным распределением токов, когда из соображений симметрии можно «угадать» общую структуру поля.
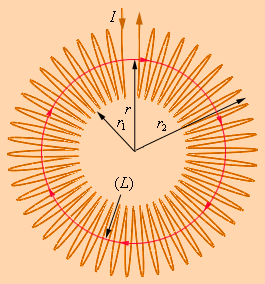
Имеется немало практически важных примеров расчета магнитных полей с помощью теоремы о циркуляции. Одним из таких примеров является задача вычисления поля тороидальной катушки (рис. 1.17.3).
|
|
| Рисунок 1.17.3.
Применение теоремы о циркуляции к тороидальной катушке
|
Предполагается, что катушка плотно, то есть виток к витку, намотана на немагнитный тороидальный сердечник. В такой катушке линии магнитной индукции замыкаются внутри катушки и представляют собой концентрические окружности. Они направлены так, что глядя вдоль них, мы увидели бы ток в витках, циркулирующим по часовой стрелке. Одна из линий индукции некоторого радиуса r1 ≤ r < r2 изображена на рис. 1.17.3. Применим теорему о циркуляции к контуру L в виде окружности, совпадающей с изображенной на рис. 1.17.3 линией индукции магнитного поля. Из соображений симметрии ясно, что модуль вектора 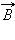 одинаков вдоль всей этой линии. По теореме о циркуляции можно записать:
одинаков вдоль всей этой линии. По теореме о циркуляции можно записать:
| B ∙ 2πr = μ0IN, |
где N – полное число витков, а I – ток, текущий по виткам катушки. Следовательно,
|
Таким образом, модуль вектора магнитной индукции в тороидальной катушке зависит от радиуса r. Если сердечник катушки тонкий, то есть r2 – r1 << r, то магнитное поле внутри катушки практически однородно. Величина n = N / 2πr представляет собой число витков на единицу длины катушки. В этом случае
|
В это выражение не входит радиус тора, поэтому оно справедливо и в предельном случае r → ∞. Но в пределе каждую часть тороидальной катушки можно рассматривать как длинную прямолинейную катушку. Такие катушки называют соленоидами. Вдали от торцов соленоида модуль магнитной индукции выражается тем же соотношением, что и в случае тороидальной катушки.
На рис. 1.17.4 изображено магнитное поле катушки конечной длины. Следует обратить внимание на то, что в центральной части катушки магнитное поле практически однородно и значительно сильнее, чем вне катушки. На это указывает густота линий магнитной индукции. В предельном случае бесконечно длинного соленоида однородное магнитное поле целиком сосредоточено внутри него.
|
|
| Рисунок 1.17.4.
Магнитное поле катушки конечной длины. В центре соленоида магнитное поле практически однородно и значительно превышает по модулю поле вне катушки
|
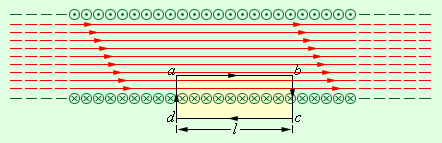
В случае бесконечно длинного соленоида выражение для модуля магнитной индукции можно получить непосредственно с помощью теоремы о циркуляции, применив ее к прямоугольному контуру, показанному на рис. 1.17.5.
|
|
| Рисунок 1.17.5.
Применение теоремы о циркуляции к расчету магнитного поля бесконечно длинного соленоида
|
Вектор магнитной индукции имеет отличную от нуля проекцию на направление обхода контура abcd только на стороне ab. Следовательно, циркуляция вектора 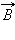 по контуру равна Bl, где l – длина стороны ab. Число витков соленоида, пронизывающих контур abcd, равно n · l, где n – число витков на единицу длины соленоида, а полный ток, пронизывающий контур, равен I n l. Согласно теореме о циркуляции,
по контуру равна Bl, где l – длина стороны ab. Число витков соленоида, пронизывающих контур abcd, равно n · l, где n – число витков на единицу длины соленоида, а полный ток, пронизывающий контур, равен I n l. Согласно теореме о циркуляции,
| B l = μ0I n l, |
откуда
|
Это выражение совпадает с полученной ранее формулой для магнитного поля тонкой тороидальной катушки.
 |
|
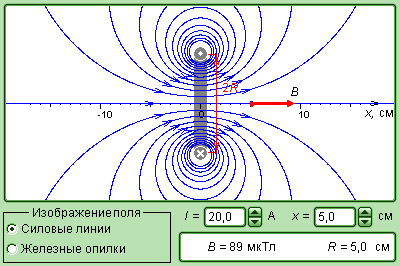
Модель. Магнитное поле кругового витка с током
|
 |
|
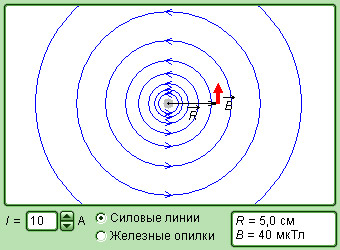
Модель. Магнитное поле прямого тока
|
 |
|
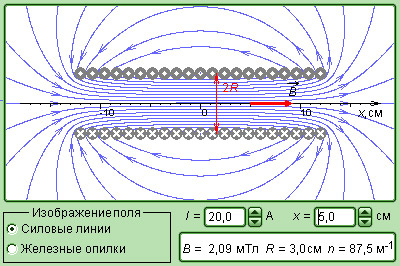
Модель. Магнитное поле соленоида
|
ЗАКОНЫ ПОСТОЯННОГО ТОКА
Электрический ток - упорядоченное движение заряженных частиц ( свободных электронов или ионов).
При этом через поперечное сечение проводника перносится эл. заряд ( при тепловом движении заряженных частиц суммарный перенесенный эл. зпряд = 0, т.к. положительные и отрицательные заряды компенсируются).
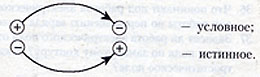
Направление эл. тока - условно принято считать направление движения положительно заряженных частиц ( от + к - ).
Действия эл. тока ( в проводнике):
тепловое действие тока - нагревание проводника ( кроме сверхпроводников);
химическое действие тока - проявляется только у электролитов, На электродах выделяются вещества, входящие в состав электролита;
магнитное действие тока ( основное ) - наблюдается у всех проводников (отклонение магнитной стрелки вблизи проводника с током и силовое действие тока на соседние проводники посредством магнитного поля).
Количественная характеристика эл. тока.
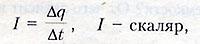
Сила тока - это отношение заряда q, перенесенного через поперечное сечение проводника за интервал времени t к этому интервалу.
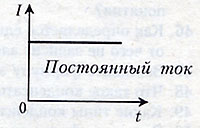
Постоянный ток - эл. ток, у которого сила тока со временем не меняется.
Сила тока зависит от заряда частицы, концентрации частиц, скорости направленного движения частиц и площади поперечного сечения проводника.
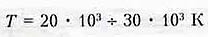
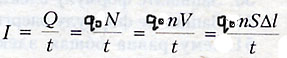
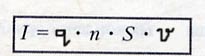
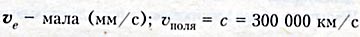
где S - площадь поперечного сечения проводника, qo - эл. заряд частицы,
n - концентрация частиц, v - скорость упорядоченного движения электронов.
Единица измерения силы тока:
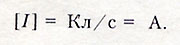
Условия, необходимые для существования электрического тока:
- наличие свободных электрически заряженных частиц;
- наличие внутри проводника эл.поля действующего с силой на заряженные частицы для их упорядоченного движения ( свободные электроны по инерции , без действия силы, перемещаться не могут из-за тормозящего воздействия на них кристаллической решетки).
Если в проводнике существует эл. поле, то между концами проводника есть разность потенциалов.
Если разность потенциалов постоянна во времени , в проводнике течет постоянный ток.
ЗАКОН ОМА ДЛЯ УЧАСТКА ЦЕПИ
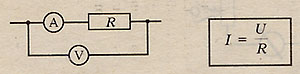
где U - напряжение на концах участка цепи, R - сопротивление участка цепи. (сам проводник тоже можно считать участком цепи).
Для каждого проводника существует своя определенная вольт-амперная характеристика.
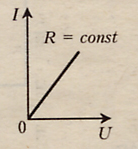
СОПРОТИВЛЕНИЕ
- основная электрическая характеристика проводника.
- по закону Ома эта величина постоянна для данного проводника.
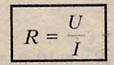
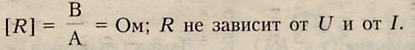
1 Ом - это сопротивление проводника с разностью потенциалов на его концах
в 1 В и силой тока в нем 1 А.
Сопротивление зависит только от свойств проводника:
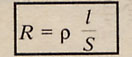
где S - площадь поперечного сечения проводника, l - длина проводника,
ро - удельное сопротивление, характеризующее свойства вещества проводника.
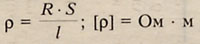
| Теорема Гаусса для вектора магнитной индукции | |
|
|
|
|
Как было показано выше, в природе нет магнитных зарядов. В 1931 г. П. Дирак высказал предположение о существовании обособленных магнитных зарядов, названных впоследствии монополи Дирака. Однако до сих пор они не найдены. Это приводит к тому, что линии вектора
В соответствии с вышеизложенным, можно сделать заключение, что поток вектора Таким образом, для любого магнитного поля и произвольной замкнутой поверхности S имеет место условие:
Это теорема Гаусса для Этот результат является математическим выражением того, что в природе нет магнитных зарядов – источников магнитного поля, на которых начинались и заканчивались бы линии магнитной индукции. Заменив поверхностный интеграл в (1.7.1) объемным, получим:
где Это условие должно выполняться для любого произвольного объема V, а это, в свою очередь, возможно, если подынтегральная функция в каждой точке поля равна нулю. Таким образом, магнитное поле обладает тем свойством, что его дивергенция всюду равна нулю:
В этом его отличие от электростатического поля, которое является потенциальным и может быть выражено скалярным потенциалом φ, магнитное поле – вихревое, или соленоидальное (см. рис. 1.3 и 1.8).
Рис. 1.9 Компьютерная модель магнитного поля Земли, подтверждающая вихревой характер, изображена на рис. 1.9.
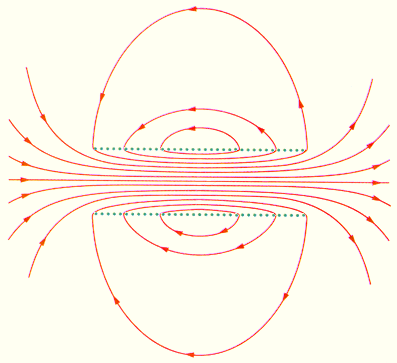
Рис 1.10 На рисунке 1.10 показаны магнитное поле постоянного магнита. Линии магнитной индукции замыкаются в окружающем пространстве. |




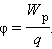
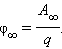
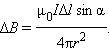
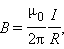
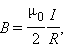
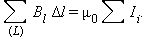
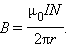
 не имеют ни начала, ни конца. Мы знаем, что поток любого вектора через поверхность равен разности числа линий, начинающихся у поверхности, и числа линий, оканчивающихся внутри поверхности:
не имеют ни начала, ни конца. Мы знаем, что поток любого вектора через поверхность равен разности числа линий, начинающихся у поверхности, и числа линий, оканчивающихся внутри поверхности: .
. ,
, (в интегральной форме): поток вектора магнитной индукции через любую замкнутую поверхность равен нулю.
(в интегральной форме): поток вектора магнитной индукции через любую замкнутую поверхность равен нулю. ,
, – оператор Лапласа.
– оператор Лапласа. или
или 


