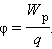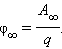1. Момент импульса материальной точки и твёрдого тела относительно точки и относительно оси. Момент силы относительно точки и относительно оси. Уравнение моментов.
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Чтобы выяснить, чем определяется характер вращения тела вокруг неподвижной оси, рассмотрим следующий опыт. Возьмем тело в виде легкой крестовины, на концах которой закреплены равные массивные грузы m (рис. 87). В центре крестовины укрепим ступенчатый шкив. Крестовину вместе со шкивом наденем на ось, позаботившись о том, чтобы трение при вращении вокруг этой оси было пренебрежимо мало.
Рис. 87. Прикрепим к одной из ступеней шкива конец нити, обмотаем ее вокруг шкива и, перебросив свободный конец нити через блок, подвесим к нему груз P. Если отпустить груз P. крестовина пойдет во вращение со все возрастающей угловой скоростью ω, причем вращение будет равномерно-ускоренным. Варьируя величину груза P, радиус шкива l, массу грузов m и их расстояние R от оси вращения» исследуем, как эти факторы влияют на величину углового ускорения 1) прямо пропорционально натяжению нити l и радиусу шкива l; 2) обратно пропорционально массе грузов т и квадрату их расстояния R от оси вращения. Следовательно, ускорение вращательного движения зависит не только от величины действующей на тело силы f, но и от расстояния l от оси вращения до литии, вдоль которой действует сила. Произведение fl дает величину так называемого момента силы относительно оси вращения. Из рассмотренного опыта следует также, что на величину углового ускорения оказывает влияние не только масса вращающегося тела, но и распределение массы относительно оси вращения. Величина, учитывающая оба эти обстоятельства, носит название момента инерции тела относительно оси вращения. Итак, для изучения вращательного движения необходимо ввести в рассмотрение две новые физические величины — момент силы и момент инерции.
Рис. 88. Начнем с выяснения понятия момента силы. Момент силы относительно точки. Моментом силы f относительно некоторой точки О называется векторная величина М, определяемая выражением
где r — радиус-вектор, проведенный из точки О в точку приложения силы. Поясняющий это определение рис. 88 выполнен в предположении, что точка О, относительно которой берется момент, и вектор f лежат в плоскости. Тогда и вектор r располагается в этой плоскости, вектор же М перпендикулярен к плоскости рисунка и направлен от нас. Вектор М изображен кружком с вписанным в него крестиком. Из определения (36.1) следует, что М является аксиальным вектором. Его направление выбрано так, что Вращение вокруг точки О в направлении силы и вектор М образуют правовинтовую систему. Модуль вектора М равен
где а — угол между направлениями векторов r и f, a
Рис. 89. Формулам (36.1) и (36.2) для момента силы и его модуля можно придать иной вид. Для этого разложим вектор силы f на две составляющие; коллинеарную с r составляющую fr и перпендикулярную к r составляющую
Первое слагаемое в полученном нами выражении равно нулю, так как векторы r и fr коллинеарны. Следовательно, момент силы относительно точки можно представить в виде:
Поскольку векторы r и
Из дистрибутивности векторного произведения вытекaeт, что момент суммы сил, имеющих общую точку приложения, равен сумме моментов слагаемых сил:
Момент пары сил. Парой сил называются две равные по величине противоположно направленные силы, не действующие вдоль одной и той же прямой (рис. 90). Расстояние l между прямыми, вдоль которых действуют
силы, называется плечом нары. Покажем» что момент пары сил относительно любой точки будет один и тот же. Сделаем это сначала для точки, лежащей в плоскости, в которой действуют силы (см. рис. 90). Обозначим одинаковый модуль сил f1 и f2 буквой f. Момент силы f1 равен fl1 и направлен на нас, момент силы f2 равен fl2 и направлен за чертеж. Результирующий момент направлен за чертеж и равен
Полученное выражение не зависит от положения точки О на плоскости, на которой лежит пара сил. Теперь выберем точку О совершенно произвольным образом (рис. 91). Проведем из этой точки радиусы-векторы r1 и r2 точек приложения сил f1 и f2. Из точки приложения силы f1 в точку приложения силы f2 проведем вектор r12. Очевидно, что
Суммарный момент сил
Заменяя r2 согласно (36.6) и использовав дистрибутивность векторного произведения, можно написать:
Поскольку f1=-f2, первые слагаемых взаимно уничтожаются и окончательно получается:
Рис. 92. Таким образом, момент нары сил перпендикулярен к плоскости, в которой лежат силы (рис. 92), и численно равен произведению модуля любой из сил на плечо. Момент силы относительно оси. Если тело может вращаться относительно точки О произвольным образом, то под действием силы f тело повернется вокруг
Рис. 93. оси, перпендикулярной к плоскости, в которой лежат сила и точка О, т. е. вокруг оси, совпадающей с направлением момента силы относительно данной точки. Величина момента характеризует способность силы вращать тело вокруг этой оси. Если тело может вращаться только вокруг некоторой фиксированной оси, способность силы вращать тело вокруг этой оси характеризуется величиной, которая называется моментом силы относительно оси. Чтобы выяснить, что такое момент силы f относительно оси, найдем момент f относительно точки О и отложим вектор М этого момента из точки О (рис 93) предполагается, что векторы f, r и М не лежат в плоскости рисунка). Проведем через точку О ось, которую мы назовем осью z, и разложим вектор М на две составляющие: Mz — параллельную оси (Составляющую Mz нужно отличать от проекции вектора М на ось z, обозначаемой символом MzMz вектор, Mz — скалярная алгебраическая величина; между нами имеется простая связь: Mz =ezMz где ez, — единичный вектор (орт) оси z) и Mz — перпендикулярную к оси. Параллельную оси z составляющую момента силы относительно точки О (лежащей на оси) называют моментом силы относительно оси. Обозначив момент силы относительно оси символом Mz, можно написать:
Рис. 94. При заданном М величина и направление вектора Mz зависят от выбора оси z. Если ось r совпадает с направлением вектора M, то Mz будет равен М, если ось, перпендикулярна к вектору М, то Mz=0. Выражение (367) для Mz можно сделать более наглядным. Для этого представим радиус-вектор r в виде суммы двух составляющих: rz — параллельной оси и R — перпендикулярной к оси (рис. 94), Тогда момент силы относительно оси z можно записать в виде
Но вектор [rz, f] перпендикулярен к оси z; следовательно, его составляющая по этой оси равна нулю. Поэтому мы приходим к формуле:
Теперь представим вектор силы f в виде суммы трех составляющих: f||—параллельной оси z, fR-коллинеарной вектору R и, наконец fx- перпендикулярной к плоскости, проходящей через ось z и вектор R. На рис. 94 эта составляющая изображена кружком с кре- Суммарный момент внутренних сил. Силы, с которыми взаимодействуют друг с другом две любые элементарные массы, лежат на одной и той же прямой (рис. 95).
Рис. 95 Их моменты относительно произвольной точки О равны по величине и противоположны по направлению. Поэтому моменты внутренних сил попарно уравновешивают друг друга, и сумма моментов всех внутренних сил для любой системы материальных точек, в частности для твердого тела, всегда равна нулю. Это утверждение справедливо как для cуммарного момента всех внутренних сил, взятого относительно любой точки» так и для Суммарного момента этих сил» взятого относительно любой оси.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2. Работа сил электростатического поля при перемещении заряда. Циркуляции вектора напряжённости. Потенциальный характер электростатического поля.
Работа в электрическом поле. Потенциал
При перемещении пробного заряда q в электрическом поле электрические силы совершают работу. Эта работа при малом перемещении 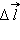 равна (рис. 1.4.1):
равна (рис. 1.4.1):
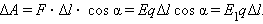 |
|
|
| Рисунок 1.4.1.
Работа электрических сил при малом перемещении
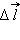 заряда q заряда q |
Рассмотрим работу сил в электрическом поле, создаваемом неизменным во времени распределенным зарядом, т.е. электростатическом поле
Электростатическое поле обладает важным свойством:
Работа сил электростатического поля при перемещении заряда из одной точки поля в другую не зависит от формы траектории, а определяется только положением начальной и конечной точек и величиной заряда.
Аналогичным свойством обладает и гравитационное поле, и в этом нет ничего удивительного, так как гравитационные и кулоновские силы описываются одинаковыми соотношениями.
Следствием независимости работы от формы траектории является следующее утверждение:
Работа сил электростатического поля при перемещении заряда по любой замкнутой траектории равна нулю.
Силовые поля, обладающие этим свойством, называют потенциальными или консервативными.
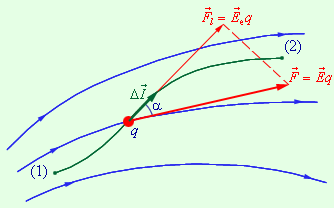
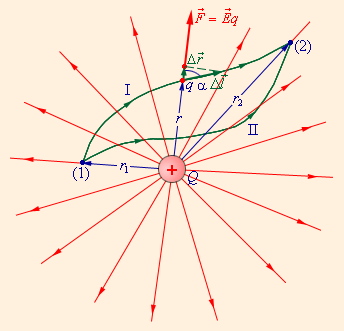
На рис. 1.4.2 изображены силовые линии кулоновского поля точечного заряда Q и две различные траектории перемещения пробного заряда q из начальной точки (1) в конечную точку (2). На одной из траекторий выделено малое перемещение 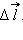 Работа ΔA кулоновских сил на этом перемещении равна
Работа ΔA кулоновских сил на этом перемещении равна
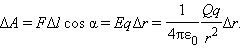 |
Таким образом, работа на малом перемещении зависит только от расстояния r между зарядами и его изменения Δr. Если это выражение проинтегрировать на интервале от r = r1 до r = r2, то можно получить
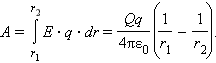 |
|
|
| Рисунок 1.4.2.
Работа кулоновских сил при перемещении заряда q зависит только от расстояний r1 и r2 начальной и конечной точек траектории
|
Полученный результат не зависит от формы траектории. На траекториях I и II, изображенных на рис. 1.4.2, работы кулоновских сил одинаковы. Если на одной из траекторий изменить направление перемещения заряда q на противоположное, то работа изменит знак. Отсюда следует, что на замкнутой траектории работа кулоновских сил равна нулю.
Если электростатическое поле создается совокупностью точечных зарядов 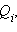 то при перемещении пробного заряда q работа A результирующего поля в соответствии с принципом суперпозиции будет складываться из работ
то при перемещении пробного заряда q работа A результирующего поля в соответствии с принципом суперпозиции будет складываться из работ 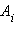 кулоновских полей точечных зарядов:
кулоновских полей точечных зарядов: 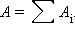 Так как каждый член суммы
Так как каждый член суммы 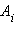 не зависит от формы траектории, то и полная работа A результирующего поля не зависит от пути и определяется только положением начальной и конечной точек.
не зависит от формы траектории, то и полная работа A результирующего поля не зависит от пути и определяется только положением начальной и конечной точек.
Свойство потенциальности электростатического поля позволяет ввести понятие потенциальной энергии заряда в электрическом поле. Для этого в пространстве выбирается некоторая точка (0), и потенциальная энергия заряда q, помещенного в эту точку, принимается равной нулю.
Потенциальная энергия заряда q, помещенного в любую точку (1) пространства, относительно фиксированной точки (0) равна работе A10, которую совершит электростатическое поле при перемещении заряда q из точки (1) в точку (0):
|
(В электростатике энергию принято обозначать буквой W, так как буквой E обозначают напряженность поля.)
Так же, как и в механике, потенциальная энергия определена с точностью до постоянной величины, зависящей от выбора опорной точки (0). Такая неоднозначность в определении потенциальной энергии не приводит к каким-либо недоразумениям, так как физический смысл имеет не сама потенциальная энергия, а разность ее значений в двух точках пространства.
Работа, совершаемая электростатическое полем при перемещении точечного заряда q из точки (1) в точку (2), равна разности значений потенциальной энергии в этих точках и не зависит от пути перемещения заряда и от выбора точки (0).
|
Потенциальная энергия заряда q, помещенного в электростатическое поле, пропорциональна величине этого заряда.
Физическую величину, равную отношению потенциальной энергии электрического заряда в электростатическом поле к величине этого заряда, называют потенциалом φ электрического поля:
|
Потенциал φ является энергетической характеристикой электростатического поля.
Работа A12 по перемещению электрического заряда q из начальной точки (1) в конечную точку (2) равна произведению заряда на разность потенциалов (φ1 – φ2) начальной и конечной точек:
| A12 = Wp1 – Wp2 = qφ1 – qφ2 = q(φ1 – φ2). |
В Международной системе единиц (СИ) единицей потенциала является вольт (В).
| 1 В = 1 Дж / 1 Кл. |
Во многих задачах электростатики при вычислении потенциалов за опорную точку (0) удобно принять бесконечно удаленную точку. В этом случае понятие потенциала может быть определено следующим образом:
Потенциал поля в данной точке пространства равен работе, которую совершают электрические силы при удалении единичного положительного заряда из данной точки в бесконечность.
|
Потенциал φ∞ поля точечного заряда Q на расстоянии r от него относительно бесконечно удаленной точки вычисляется следующим образом:
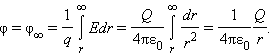 |
Как следует из теоремы Гаусса, эта же формула выражает потенциал поля однородно заряженного шара (или сферы) при r ≥ R, где R – радиус шара.
Для наглядного представления электростатическое поля наряду с силовыми линиями используют эквипотенциальные поверхности.
Поверхность, во всех точках которой потенциал электрического поля имеет одинаковые значения, называется эквипотенциальной поверхностью или поверхностью равного потенциала.
Силовые линии электростатическое поля всегда перпендикулярны эквипотенциальным поверхностям.
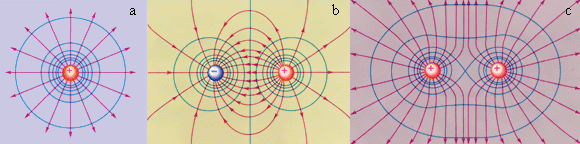
Эквипотенциальные поверхности кулоновского поля точечного заряда – концентрические сферы. На рис. 1.4.3 представлены картины силовых линий и эквипотенциальных поверхностей некоторых простых электростатических полей.
|
|
| Рисунок 1.4.3.
Эквипотенциальные поверхности (синие линии) и силовые линии (красные линии) простых электрических полей: a – точечный заряд; b – электрический диполь; c – два равных положительных заряда
|
В случае однородного поля эквипотенциальные поверхности представляют собой систему параллельных плоскостей.
Если пробный заряд q совершил малое перемещение 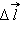 вдоль силовой линии из точки (1) в точку (2), то можно записать:
вдоль силовой линии из точки (1) в точку (2), то можно записать:
| ΔA12 = qEΔl = q(φ1 – φ2) = – qΔφ, |
где Δφ = φ1 – φ2 – изменение потенциала. Отсюда следует
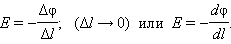 |
Это соотношение в скалярной форме выражает связь между напряженностью поля и потенциалом. Здесь l – координата, отсчитываемая вдоль силовой линии.
Из принципа суперпозиции напряженностей полей, создаваемых электрическими зарядами, следует принцип суперпозиции для потенциалов:
| φ = φ1 + φ2 + φ3 + ... |
Циркуляцией вектора напряженности называется работа, которую совершают электрические силы при перемещении единичного положительного заряда по замкнутому пути L
 |
(13.18) |
Так как работа сил электростатического поля по замкнутому контуру равна нулю (работа сил потенциального поля), следовательно циркуляция напряженности электростатического поля по замкнутому контуру равна нулю.

3. Уравнение плоскостей и сферической бегущих волн. Волновое число
Уравнением волны называется выражение, которое дает смещение колеблющейся точки как функцию ее координат (x, y, z) и времени t.
 . . |
(5.2.1) |
Эта функция должна быть периодической как относительно времени, так и координат (волна – это распространяющееся колебание, следовательно периодически повторяющееся движение). Кроме того, точки, отстоящие друг от друга на расстоянии l, колеблются одинаковым образом.
Уравнение плоской волны
Найдем вид функции x в случае плоской волны, предполагая, что колебания носят гармонический характер.
Направим оси координат так, чтобы ось x совпадала с направлением распространения волны. Тогда волновая поверхность будет перпендикулярна оси x. Так как все точки волновой поверхности колеблются одинаково, смещение x будет зависеть только от х и t:  . Пусть колебание точек, лежащих в плоскости
. Пусть колебание точек, лежащих в плоскости  , имеет вид (при начальной фазе
, имеет вид (при начальной фазе  )
)
  |
(5.2.2) |
Найдем вид колебания частиц в плоскости, соответствующей произвольному значению x. Чтобы пройти путь x, необходимо время  .
.
Следовательно, колебания частиц в плоскости x будут отставать по времени на t от колебаний частиц в плоскости  , т.е.
, т.е.
 , , |
(5.2.3) |
– это уравнение плоской волны.
Таким образом, x есть смещение любой из точек с координатой x в момент времени t. При выводе мы предполагали, что амплитуда колебания  . Это будет, если энергия волны не поглощается средой.
. Это будет, если энергия волны не поглощается средой.
Такой же вид уравнение (5.2.3) будет иметь, если колебания распространяются вдоль оси y или z.
В общем виде уравнение плоской волны записывается так:
 , или , или  . . |
(5.2.4) |
Выражения (5.2.3) и (5.2.4) есть уравнения бегущей волны.
Уравнение (5.2.3) описывает волну, распространяющуюся в сторону увеличения x. Волна, распространяющаяся в противоположном направлении, имеет вид:
 .
.
Уравнение волны можно записать и в другом виде.
Введем волновое число  , или в векторной форме:
, или в векторной форме:
 , , |
(5.2.5) |
где  – волновой вектор,
– волновой вектор,  – нормаль к волновой поверхности.
– нормаль к волновой поверхности.
Так как  , то
, то  . Отсюда
. Отсюда  . Тогда уравнение плоской волны запишется так:
. Тогда уравнение плоской волны запишется так:
 . . |
(5.2.6) |
Уравнение сферической волны
В случае, когда скорость волны υ во всех направлениях постоянна, а источник точечный, волна будет сферической.
Предположим, что фаза колебаний источника равна wt (т.е.  ). Тогда точки, лежащие на волновой поверхности радиуса r, будут иметь фазу
). Тогда точки, лежащие на волновой поверхности радиуса r, будут иметь фазу  . Амплитуда колебаний здесь, даже если волна не поглощается средой, не будет постоянной, она убывает по закону
. Амплитуда колебаний здесь, даже если волна не поглощается средой, не будет постоянной, она убывает по закону  . Следовательно, уравнение сферической волны:
. Следовательно, уравнение сферической волны:
 , или , или  , , |
(5.2.7) |
где А равна амплитуде на расстоянии от источника равном единице.
Уравнение (5.2.7) неприменимо для малых r, т.к. при  , амплитуда стремится к бесконечности. То, что амплитуда колебаний
, амплитуда стремится к бесконечности. То, что амплитуда колебаний  , следует из рассмотрения энергии, переносимой волной.
, следует из рассмотрения энергии, переносимой волной.
ВОЛНОВОЕ ЧИСЛО - модуль волнового вектора; определяет пространственный период волны (длину волны 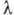 ) в направлении её распространения:
) в направлении её распространения: 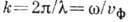 (где
(где 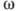 - круговая частота,
- круговая частота, 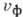 - фазовая скорость волны). В оптике и спектроскопии В. ч. часто наз. величину, обратную длине волны,
- фазовая скорость волны). В оптике и спектроскопии В. ч. часто наз. величину, обратную длине волны,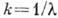



 . Результаты подобного исследования сводятся к тому, что угловое ускорение
. Результаты подобного исследования сводятся к тому, что угловое ускорение 


 — длина перпендикуляра, опущенного из точки О на прямую, вдоль которой действует сила (см, рис. 88). Эта длина называется плечом силы относительно точки О.
— длина перпендикуляра, опущенного из точки О на прямую, вдоль которой действует сила (см, рис. 88). Эта длина называется плечом силы относительно точки О.
 (рис. 89). Если представить себе окружность радиуса r с центром в точке О, то составляющая fr будет направлена по касательной к окружности. Заменим в формуле (36.1) вектор f суммой
(рис. 89). Если представить себе окружность радиуса r с центром в точке О, то составляющая fr будет направлена по касательной к окружности. Заменим в формуле (36.1) вектор f суммой  и воспользуемся свойством дистрибутивности векторного произведения:
и воспользуемся свойством дистрибутивности векторного произведения:






 и
и  равен
равен











 , модуль вектора момента импульса можно записатьв виде:
, модуль вектора момента импульса можно записатьв виде:




 равен вектору скорости v и, следовательно, совпадает по направлению с вектором р=mv. Вектор
равен вектору скорости v и, следовательно, совпадает по направлению с вектором р=mv. Вектор  по второму закону Ньютона равен действующей на тело силе f [см. (22.3)]. Следовательно, выражение (37.5) можно написать так:
по второму закону Ньютона равен действующей на тело силе f [см. (22.3)]. Следовательно, выражение (37.5) можно написать так:


 ].
].
 ).
).
 , результирующий момент внешних сил, действующих на ту же точку, — символом Мi. Тогда уравнение (37.6) для i-й материальной точки будет иметь вид:
, результирующий момент внешних сил, действующих на ту же точку, — символом Мi. Тогда уравнение (37.6) для i-й материальной точки будет иметь вид: (i=1, 2,…, N)
(i=1, 2,…, N)