Пусть функция 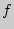 определена в некоторой окрестности
определена в некоторой окрестности 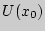 токи
токи 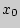 , непрерывна в этой точке и
, непрерывна в этой точке и 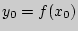 , а
, а 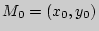 (рис.2).
(рис.2).
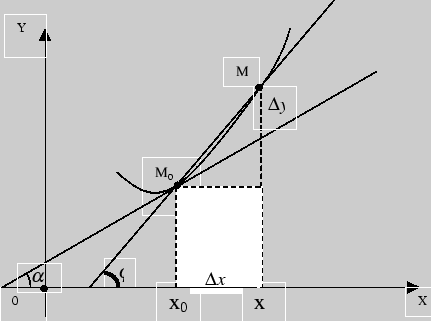
Рис. 2
Придав произвольное приращение аргументу 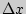 , так чтобы
, так чтобы 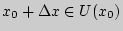 , перейдем к точке
, перейдем к точке 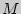 с абсциссой
с абсциссой 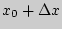 и ординатой
и ординатой 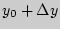 , где
, где 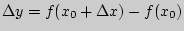 .
.
Уравнение прямой, проходящей через точки 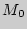 и
и 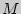 (секущей графика функции
(секущей графика функции 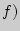 , имеет вид:
, имеет вид: 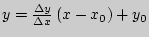 , где отношение
, где отношение 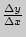 представляет собой угловой коэффициент секущей (
представляет собой угловой коэффициент секущей (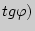 .
.
Касательной к графику функции 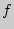 в точке
в точке 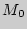 называется предельное положение секущей
называется предельное положение секущей 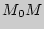 , при стремлении точки
, при стремлении точки 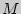 по графику
по графику 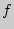 к точке
к точке 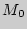 .
.
Для того, чтобы секущая 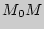 при
при  стремилась к предельному положению, отличному от вертикальной прямой , необходимо и достаточно, чтобы существовал конечный предел
стремилась к предельному положению, отличному от вертикальной прямой , необходимо и достаточно, чтобы существовал конечный предел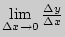 , то есть , чтобы существовала конечная производная функции
, то есть , чтобы существовала конечная производная функции 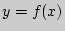 в точке
в точке 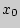 .
.
Угловой коэффициент касательной получается путем перехода от 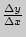 к пределу при
к пределу при  :
:
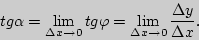
Таким образом, получим, что 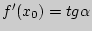 , где
, где 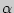 - угол наклона касательной к оси
- угол наклона касательной к оси 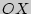 (см. рис.), а значение производной равно угловому коэффициенту касательной к графику функции. В этом заключается геометрический смысл производной. Уравнение касательной к графику функции
(см. рис.), а значение производной равно угловому коэффициенту касательной к графику функции. В этом заключается геометрический смысл производной. Уравнение касательной к графику функции 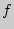 в точке
в точке 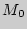 имеет вид
имеет вид
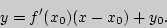
В случае бесконечной производной 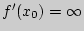 .
.
Из уравнения секущей имеем:
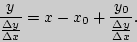
Переходя в равенстве к пределу при  , получаем уравнение касательной к графику функции в точке
, получаем уравнение касательной к графику функции в точке 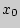 в виде
в виде 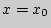 , то есть касательная является в данном случае вертикальной прямой, проходящей через точку
, то есть касательная является в данном случае вертикальной прямой, проходящей через точку 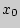 оси абсцисс.
оси абсцисс.
Пусть материальная точка движется прямолинейно и 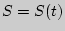 - длина пути, проходимого за время
- длина пути, проходимого за время 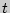 , отсчитываемого от некоторого момента времени
, отсчитываемого от некоторого момента времени 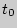 .
.
Для определения скорости 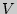 в данный момент
в данный момент 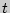 придадим переменной
придадим переменной 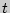 некоторое приращение
некоторое приращение 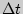 , при этом приращение пути будет равно
, при этом приращение пути будет равно 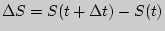 .
.
Отношение 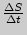 называется в физике величиной средней скорости движения за промежуток времени, начиная с момента времени
называется в физике величиной средней скорости движения за промежуток времени, начиная с момента времени 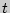 , и обозначается
, и обозначается
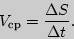
Предел 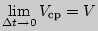 называется величиной мгновенной скорости движения в момент времени
называется величиной мгновенной скорости движения в момент времени 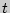 .
.
Таким образом, мгновенная скорость в момент времени 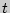 прямолинейного движения, совершаемого по закону
прямолинейного движения, совершаемого по закону 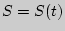 равна значению производной
равна значению производной 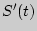 .
.
Примеры задач
Задача 1. Составьте уравнение общей касательной к графикам функций 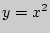 и
и 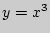 .
.
Решение.
I способ.
Прямая 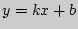 является общей касательной графиков функций
является общей касательной графиков функций 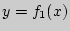 и
и 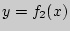 , если она касается как одного, так и другого графиков, но совершенно не обязательно в одной и той же точке.
, если она касается как одного, так и другого графиков, но совершенно не обязательно в одной и той же точке.
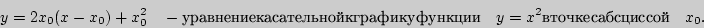
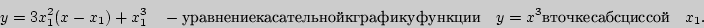
Прямые совпадают, если их угловые коэффициенты и свободные члены равны. Отсюда
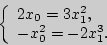
Решением системы будут

Уравнения общих касательных имеют вид:
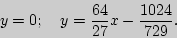
II способ.
Уравнение касательной к кривой 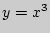 в точке с абсциссой
в точке с абсциссой 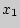 имеет вид:
имеет вид:
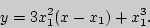
Для касания прямой 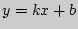 параболы
параболы 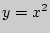 достаточно, чтобы дискриминант квадратного уравнения
достаточно, чтобы дискриминант квадратного уравнения 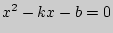 был равен нулю.
был равен нулю.
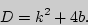
Заметим, что: 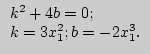
Получаем 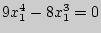
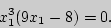
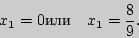
Ответ: Уравнения общих касательных имеют вид: 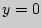 и
и 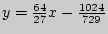 .
.

