Характеристики вращательного движения: угловой закон движения, угловые скорость и ускорение. Связь угловых и линейных характеристик. Моменты

Характеристики вращательного движения:

угловой закон движения
Угловой скоростью называют векторную величину, характеризующую быстроту вращения твердого тела, определяемую как приращение угла поворота тела за промежуток времени.
Рассмотрим бесконечно малый промежуток времени Δt → 0, за который твердое тело совершает поворот на бесконечно малый угол Δα вокруг мгновенной оси Ω
Предел, к которому стремится отношение Δα / Δt, называется угловой скоростью твердого тела в рассматриваемый момент времени

Угловая скорость является векторной величиной. Вектор угловой скорости ω может быть приложен к любой точке мгновенной оси и направлен в каждый момент времени по мгновенной оси Ω, так, чтобы, смотря навстречу этому вектору, видеть вращение тела происходящим против движения часовой стрелки.

Угловая скорость вращения тела — векторная величина.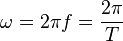 $\omega = {2 \pi f} = {2 \pi \over T}$ .
Угловым ускорением называется векторная величина, равная первой производной угловой скорости по времени:

При вращении тела вокруг неподвижной оси вектор углового ускорения направлен вдоль оси вращения в сторону вектора элементарного приращения угловой скорости. При ускоренном движении вектор

 сонаправлен вектору  (рис.8), при замедленном.— противонаправлен ему (рис. 9).
Связь угловых и линейных характеристик

Тангенциальная составляющая ускорения

Нормальная составляющая ускорения

Таким образом, связь между линейными (длина пути s, пройденного точкой по дуге окружности радиуса R, линейная скорость v, тангенциальное ускорение а, нормальное ускорение аn) и угловыми величинами (угол поворота , угловая скорость (о, угловое ускорение ) выражается следующими формулами:

В случае равнопеременного движения точки по окружности (=const)
Момент инерции — скалярная физическая величина, мера инертности во вращательном движении вокруг оси. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).

Единица измерения в Международной системе единиц (СИ): кг·м².
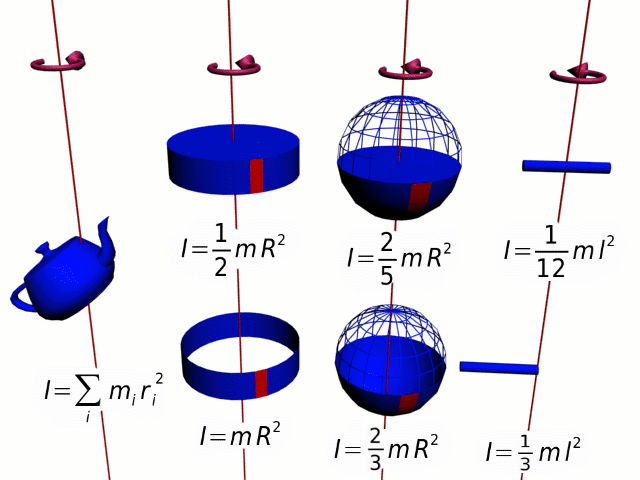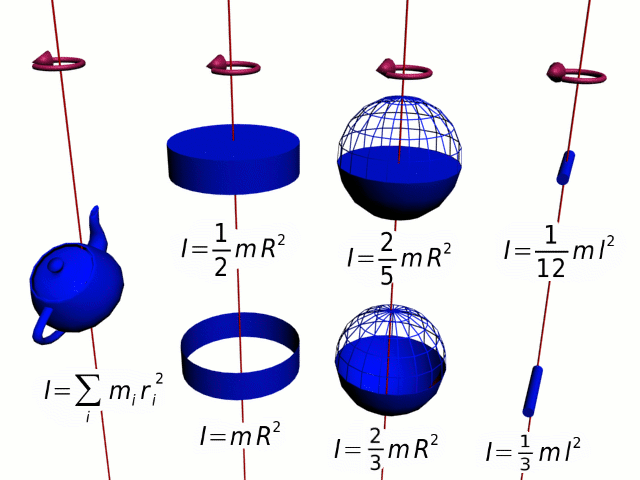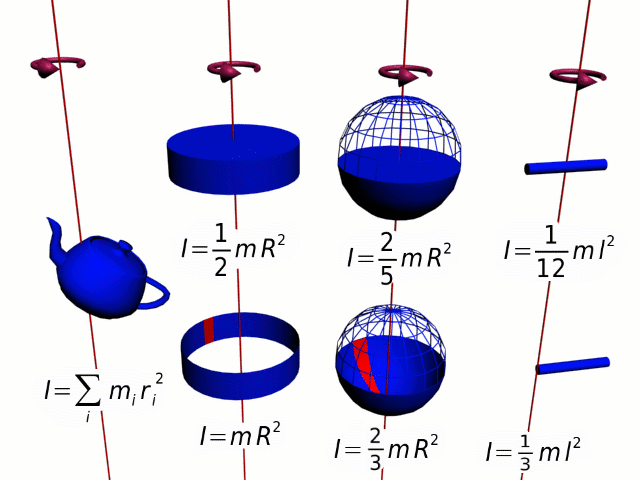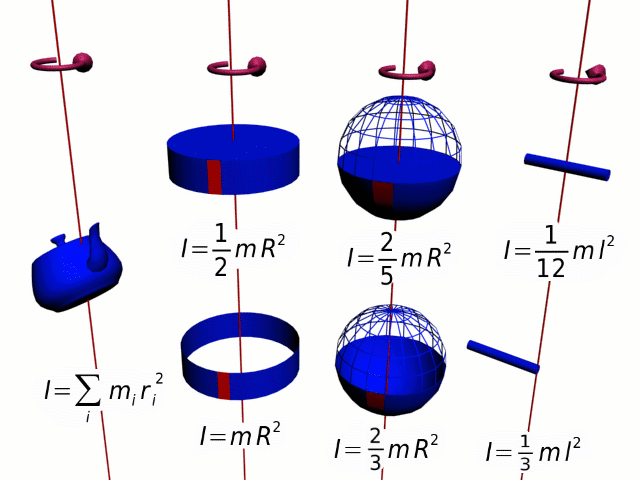
Момент импульса 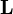$\mathbf L$ материальной точки относительно некоторого начала отсчёта определяется векторным произведением её радиус-вектора и импульса: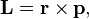

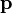$~\mathbf{L}=\mathbf{r}\times\mathbf{p},$

где $~\mathbf r$ — радиус-вектор частицы относительно выбранного неподвижного в данной системе отсчёта начала отсчёта, $~\mathbf p$ — импульс частицы.

Для нескольких частиц момент импульса определяется как (векторная) сумма таких членов:

$~\mathbf{L}=\sum_i\mathbf{r}_i\times\mathbf{p}_i,$

где $~\mathbf r_i, \mathbf p_i$ — радиус-вектор и импульс каждой частицы, входящей в систему, момент импульса которой определяется.

(В пределе количество частиц может быть бесконечным, например, в случае твердого тела с непрерывно распределенной массой или вообще распределенной системы это может быть записано как $~\mathbf{L}=\int\mathbf{r}\times\mathbf{dp},$ где $\mathbf{dp}$ — импульс бесконечно малого точечного элемента системы).

В системе СИ момент импульса измеряется в единицах джоуль-секунда; Дж·с.

Из определения момента импульса следует его аддитивность: как, для системы частиц в частности, так и для системы, состоящей из нескольких подсистем, выполняется:

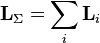$\mathbf{L}_\Sigma = \sum\limits_i \mathbf{L}_i$ .