производная по направлению — это обобщение понятия производной наслучай функции нескольких переменных. Производная по направлению показывает, насколько быстрофункция изменяется при движении вдоль заданного направления.
Производная функции одной переменной показывает, как изменяется её значение при малом измененииаргумента. Если мы попытаемся по аналогии определить производную функции многих переменных, тостолкнёмся с трудностью: в этом случае изменение аргумента (то есть точки в пространстве) можетпроисходить в разных направлениях, и при этом будут получаться разные значения производной. Именноэто соображение и приводит к определению производной по направлению.
Рассмотрим функцию двух переменных n=2; z=f(x, y). Под направлением мы будем понимать любой вектор 
на плоскости.
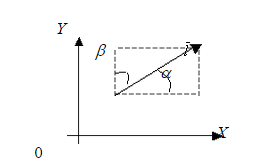
Определение 1. Направляющими косинусами данного направления 
называются косинусы углов, которые данное направление образуют с положительными направлениями осей координат. Направляющие косинусы данного направления -
.
Направляющие косинусы любого направления в любом пространстве обладают следующим свойством: сумма квадратов направляющих косинусов равна единице.
.
На плоскости имеем
.
.
Если рассмотреть вектор 
, координатами которого являются направляющие косинусы данного направления, то этот вектор сонаправлен с вектором 
и имеет единичную длину.
Пусть даны точка 
и направление 
. Переместим точку М0 вдоль направления 
на величину Dl в точку М1. Тогда функция и аргумент получат соответствующие приращения.
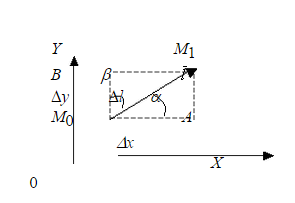
Функция получит приращение, которое называется приращением функции в данном направлении: 
,
Из треугольника М0 М1 А: 
.
Из треугольника М0 М1 В: 
.
.
