Промежутки монотонности функции, их нахождение.

Монотонность функций

Определение возрастающей и убывающей функции

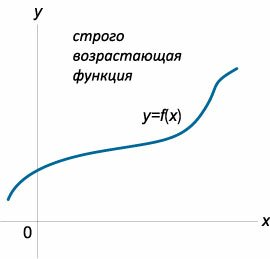
Пусть y = f(x) является дифференцируемой функцией на интервале (a, b). Функция называется возрастающей(или неубывающей) на данном интервале, если для любых точек x1, x2 ∈ (a, b), таких, что x1< x2, выполняется неравенство f(x1) ≤ f(x2).

Если данное неравенство является строгим, т.е. f(x1) < f(x2), то говорят, что функция y = f(x) является строго возрастающей на интервале (a, b).

Аналогично определяются убывающая (или невозрастающая) и строго убывающая функции.

Введенные понятия можно сформулировать в более компактной форме. Функция y = f(x) называется

возрастающей (неубывающей) на интервале (a, b), если
∀ x1, x2 ∈ (a, b) : x1< x2 ⇒ f(x1) ≤ f(x2);
строго возрастающей на интервале (a, b), если
∀ x1, x2 ∈ (a, b) : x1< x2 ⇒ f(x1) < f(x2);
убывающей (невозрастающей) на интервале (a, b), если
∀ x1, x2 ∈ (a, b) : x1< x2 ⇒ f(x1) ≥ f(x2);
строго убывающей на интервале (a, b), если
∀ x1, x2 ∈ (a, b) : x1< x2 ⇒ f(x1) > f(x2).

Ясно, что неубывающая функция может содержать участки строгого возрастания и интервалы, где функция является постоянной. Схематически это иллюстрируется на рисунках 1-4.


Рис.1		Рис.2


Рис.3		Рис.4

Если функция f(x) дифференцируема на интервале (a, b) и принадлежит к одному из четырех рассмотренных типов (т.е. является возрастающей, строго возрастающей, убывающей или строго убывающей), то такая функция называется монотонной на данном интервале.

Понятия возрастания и убывания функции можно определить также и для отдельной точки x0. В этом случае рассматривается малая δ-окрестность (x0 − δ, x0 + δ) этой точки. Функция y = f(x) является строго возрастающей в точке x0, если существует число δ > 0, такое, что

∀ x ∈ (x0 − δ, x0) ⇒ f(x) < f(x0);

∀ x ∈ (x0, x0 + δ) ⇒ f(x) > f(x0).

Аналогичным образом определяется строгое убывание функции y = f(x) в точке x0.

http://www.math24.ru/monotonic-functions.html