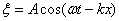Упругие волны. Описание плоской волны. Длина волны и волновой вектор

колеблющиеся тело, помещенное в упругую среду, является источником колебаний, распространяющихся от него во все стороны. Процесс распространения колебаний в среде называется волной.

Волны бывают поперечными (колебания происходят в плоскости, перпендикулярной направлению распространения), и продольными (сгущение и разряжение частиц среды происходят в направлении распространения).

Уравнением волны называется выражение, которое дает смещение колеблющейся точки как функцию ее координат (x, y, z) и времени t.

та функция должна быть периодической как относительно времени, так и координат (волна – это распространяющееся колебание, следовательно периодически повторяющееся движение). Кроме того, точки, отстоящие друг от друга на расстоянии l, колеблются одинаковым образом.

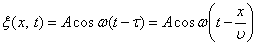
– это уравнение плоской волны.
Такой же вид уравнение (5.2.3) будет иметь, если колебания распространяются вдоль оси y или z
В общем виде уравнение плоской волны записывается так:

Выражения (5.2.3) и (5.2.4) есть уравнения бегущей волны

Введем волновое число  , или в векторной форме:

где 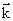 – волновой вектор,  – нормаль к волновой поверхности.

Так как  , то 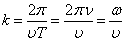 . Отсюда  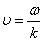. Тогда уравнение плоской волны запишется так:

ВОЛНОВОЙ ВЕКТОР - вектор k, определяющий направление распространения и пространственный период плоской монохроматич. Волны

где 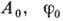 - постоянные амплитуда и фаза волны,  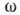- круговая частота, r - радиус-вектор. Модуль В. в. наз. волновым числом k=  , где 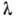 - пространственный период или длина волны. В направлении В. в. происходит наибыстрейшее изменение фазы волны  , поэтому оно и принимается за направление распространения. Скорость перемещения фазы в этом направлении, или фазовая скорость 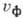 , определяется через волновое число 

23)