Дивергенция векторного поля. I и II уравнения Максвелла (rotE, rotH), ток смещения

Дивергенцией или расходимостью векторного поля a(M)  называется скалярная функция, определяемая равенством:

Уравнения Максвелла—основные уравнения электродинамики — были впервые сформулированы Дж. Максвеллом в 1860-х годах.

Из выражений

H = rot A,  Е = −   − grad φ

легко получить уравнения, содержащие только E и H. Для этого определим rotE:

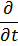rot Е = −   rot A − rot grad φ.

Но ротор всякого градиента равен нулю; следовательно,

rot Е = −  .                                        (26.1)

Взяв дивергенцию от обеих частей уравнения rot Н=А и помня, что дивергенция всякого ротора равна нулю, находим

div Н = 0

равнения (26.1), (26.2) можно написать в интегральной форме. Согласно теореме Гаусса

div H dV =  H df,

Интеграл от вектора по некоторой поверхности называется потоком вектора через эту поверхность. Таким образом, поток магнитного поля через всякую замкнутую поверхность равен нулю.

rotH=j+ E

Если замкнуть ключ (рис. 6.1), то лампа при постоянном токе гореть не будет: емкость C – разрывает цепь постоянного тока. Но вот в моменты включения лампа будет вспыхивать.

Для установления количественных соотношений между изменяющимся электрическим полем и вызываемым им магнитным полем Максвелл ввел в рассмотрение ток смещения.

Максвелл сделал вывод: всякое переменное электрическое поле порождает переменное магнитное поле.

      Токи проводимости в проводнике замыкаются токами смещения в диэлектрике или в вакууме. Переменное электрическое поле в конденсаторе создает такое же магнитное поле, как если бы между обкладками существовал ток проводимости, имеющий величину, равную току в металлическом проводнике

D=Eee0

I=q=DS S- площадь обкладки

16)