Циркуляция векторного поля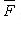. Циркуляция электростатического и магнитостатического полей.

Циркуляция векторного поля  вдоль контура l - линейный интеграл вдоль замкнутой линии l: 

или в векторной форме

где n единичный вектор нормали к поверхности S, направление которого таково, что при обходе контура l = дS поверхность S остается слева.

Циркуляцией вектора напряженности называется работа, которую совершают электрические силы при перемещении единичного положительного заряда по замкнутому пути L

Так как работа сил электростатического поля по замкнутому контуру равна нулю (работа сил потенциального поля), следовательно циркуляция напряженности электростатического поля по замкнутому контуру равна нулю.

Циркуляция магнитного поля постоянных токов по всякому замкнутому контуру пропорциональна сумме сил токов, пронизывающих контур циркуляции.

В математической формулировке для магнитостатики теорема имеет следующий вид:

Здесь 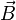 — вектор магнитной индукции,  — плотность тока; интегрирование слева производится по произвольному замкнутому контуру, справа — по произвольной поверхности, натянутой на этот контур. Данная форма носит название интегральной, поскольку в явном виде содержит интегрирование. Теорема может быть также представлена в дифференциальной форме[4]:

15