Критерий Гурвица. Для того чтобы система была устойчива, необходимо и достаточно, чтобы, все определители Гурвица, составленные из коэффициентов ее характеристического уравнения, были больше нуля (при а0 > 0):
, 
.
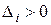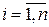Из этого критерия следует, что при n = 3 необходимое и достаточное условие устойчивости имеет вид
, 
, 
, 
.
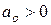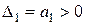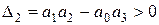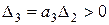Следовательно, уже при п = 3 необходимое условие устойчивости (5.12) не является и достаточным. Для устойчивости систем третьего порядка кроме необходимого условия должно выполняться неравенство 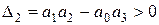(т.е. разность между произведением средних коэффициентов и произведением крайних коэффициентов должна быть положительной).
Критерий Льенара — Шипара. При выполненнии необходимого условия для устойчивости системы необходимо и достаточно, чтобы были положительны или все определители Гурвица с четными индексами, или все определители Гурвица с нечетными индексами.
Следовательно, для того чтобы система была устойчива, необходимо и достаточно, чтобы
, 
, …, 
; 
, 
, 
, …
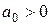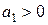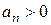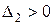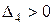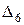или
, , …, ; 
, 
, 
, …
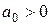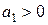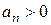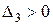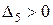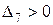Таким образом, для исследования устойчивости нет необходимости вычислять все определители Гурвица.
Частотные критерии устойчивости
Частотными критериями называются критерии устойчивости, основанные на построении частотных характеристик и так называемой кривой Михайлова. Ниже рассмотрены следующие частотные критерии: критерий Михайлова, Найквиста и логарифмический частотный критерий.
Пусть характеристический полином
.
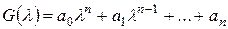Подставим в него
.
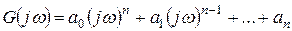Кривую, которую описывает конец вектора 
на комплексной плоскости при изменении 
от 0 до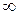 
, называют кривой Михайлова.
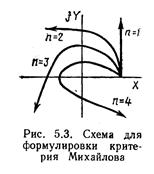
Критерий Михайлова. Для того чтобы система была устойчива, необходимо и достаточно, чтобы кривая Михайлова, начинаясь при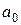 
> 0 с действительной положительной полуоси, при возрастании 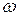от 0 до 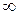последовательно обходила п квадрантов в положительном направлении, не попадая в начало координат (рис. 5.3).
Если непрерывная система имеет конечный граничный коэффициент, то включение импульсного звена уменьшает его. Но это справедливо, если амплитудно-фазовая характеристика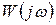 
разомкнутой системы при высоких частотах не имеет существенной части в правой полуплоскости, т. е. характеристика 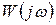при высоких частотах не проходит в первом и четвертом квадрантах или в этих квадрантах модуль | 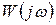| пренебрежимо мал.
Если характеристика 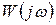при высоких частотах имеет существенную часть в правой полуплоскости, что возможно при наличии в системе элемента чистого запаздывания, включение импульсного элемента с надлежащим периодом Ти повышает запас устойчивости и соответственно увеличивает граничный передаточный коэффициент. Иначе: непрерывные системы со значительным запаздыванием можно стабилизировать путем введения импульсного элемента.
Алгебраическими критериями называются критерии, которые основаны на проверке определенных соотношений, составленных из коэффициентов характеристического уравнения. Поэтому при использовании алгебраических критериев нужно иметь только характеристическое уравнение. Если исследование устойчивости проводится с помощью алгебраических критериев, нужно прежде всего проверить выполнение необходимого условия устойчивости, так как его проверка не требует никаких вычислений и при невыполнении этого условия дальнейших исследований проводить не нужно.
