Понятие интеграла может быть расширено на функции двух и большего числа переменных. Рассмотрим, например, функцию двух переменных z = f (x,y) . Двойной интеграл от функции f (x,y) обозначается как
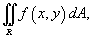
где R - область интегрирования в плоскости Oxy. Если определенный интеграл 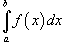 от функции одной переменной
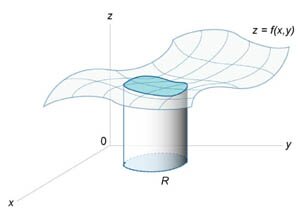
от функции одной переменной 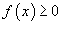 выражает площадь под кривой f (x) в интервале от x = a до x = b , то двойной интеграл выражает объем под поверхностью z = f (x,y) выше плоскости Oxy в области интегрирования R (рисунок 1).
выражает площадь под кривой f (x) в интервале от x = a до x = b , то двойной интеграл выражает объем под поверхностью z = f (x,y) выше плоскости Oxy в области интегрирования R (рисунок 1).
 решение двойного интеграла сводится к решению двукратного.
Алгоритм решения двойного интеграла:Систематизируем информацию: в каком порядке нужно решать рассматриваемую задачу? 1) Необходимо выполнить чертёж. Без чертежа задачу не решить. Точнее, решить можно, но это будет похоже на игру в шахматы вслепую. На чертеже следует изобразить область 2) Расставить пределы интегрирования и перейти к повторным интегралам. 3) Взять внутренний интеграл 4) Взять внешний интеграл и получить ответ (число). |

