несобственные интегралы

http://mathprofi.ru/nesobstvennye_integraly.html

Определенный интеграл 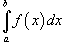называется несобственным интегралом, если выполняется, по крайней мере, одно из следующих условий:

Пусть f (x) является непрерывной функцией в интервале [a, ?). Несобственный интеграл определяется через предел следующим образом:

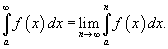
Рассмотрим также случай, когда функция f (x) непрерывна в интервале (??, b]. В этом случае несобственный интеграл определяется как

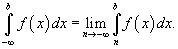
Если указанные выше пределы существуют и конечны, то говорят что несобственные интегралы сходятся.
В противном случае интегралы расходятся.

Пусть f (x) является непрерывной функцией на множестве действительных чисел. Тогда справедливо соотношение

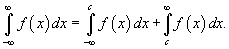
Если для некоторого действительного числа c оба интеграла в правой части сходятся, то говорят, что интеграл 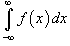также сходится; в противном случае он расходится.

Пусть функция f (x) непрерывна в интервале [a,b), но имеет разрыв в точке x = b. В этом случае несобственный интеграл определяется в виде

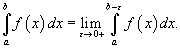
Аналогично можно рассмотреть случай, когда функция f (x) непрерывна в интервале (a,b], но имеет разрыв при x = a. Тогда

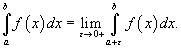
Если приведенные выше пределы существуют и конечны, то говорят, что соответствующие несобственные интегралы сходятся. В противном случае они считаются расходящимися.

Пусть f (x) непрерывна для всех действительных x в интервале [a,b], за исключением некоторой точки 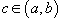. Тогда справедливо соотношение

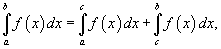
и говорят, что несобственный интеграл 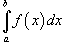сходится, если оба интеграла в правой части верхнего равенства сходятся. В противном случае несобственный интеграл расходится.