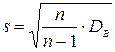Для того чтобы охарактеризовать рассеяние значений количественного признака X генеральной совокупности вокруг своего среднего значения, вводят сводную характеристику - генеральную дисперсию.
Генеральной дисперсией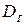 
называют среднее арифметическое квадратов отклонений значений признака генеральной совокупности от их среднего значения 
.
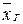Если все значения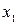 
, 
, ..., 
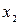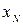признака генеральной совокупности объема N различны, то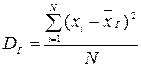 
Если же значения признака , , ...,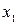 
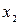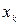имеют соответственно частоты 
, 
, ..., 
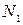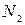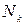, причем 
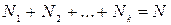, то 
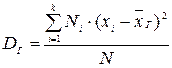
Пример 1. Генеральная совокупность задана таблицей распределения:
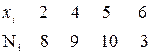
Найти генеральную дисперсию.
Решение: Найдем генеральную среднюю:
.
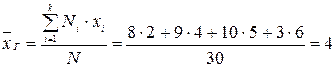Найдем генеральную дисперсию:
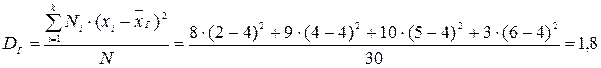
Кроме дисперсии для характеристики рассеяния значений признака генеральной совокупности вокруг своего среднего значения пользуются сводной характеристикой - средним квадратическим отклонением.
Генеральным средним квадратическим отклонением (стандартом) называют квадратный корень из генеральной дисперсии: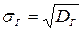 
.
Для того чтобы охарактеризовать рассеяние наблюдаемых значений количественного признака выборки вокруг своего среднего значения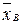 
вводят сводную характеристику - выборочную дисперсию.
Выборочной дисперсией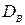 
называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения .
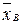Если все значения , , ...,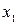 
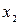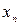признака выборки объема n различны, то
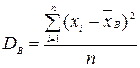
Если же значения признака 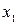, , 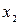..., 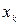имеют соответственно частоты 
, 
, ..., 
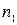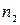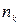, причем 
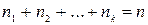, то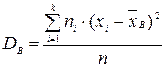 
.
Пример 2. Выборочная совокупность задана таблицей распределения:
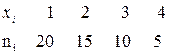
Найти выборочную дисперсию.
Решение: Найдем выборочную среднюю:
.
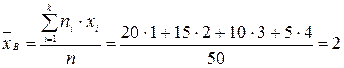Найдем выборочную дисперсию:
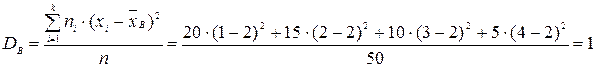
Кроме дисперсии для характеристики рассеяния значений признака выборочной совокупности вокруг своего среднего значения пользуются сводной характеристикой - средним квадратическим отклонением.
Выборочным средним квадратическим отклонением (стандартом) называют квадратный корень из выборочной дисперсии: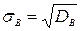 
Вычисление дисперсии, безразлично - выборочной или генеральной, можно упростить, используя следующую теорему.
Теорема. Дисперсия равна среднему квадратов значений признака минус квадрат общей средней: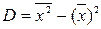 
.
Пример. Найти выборочную дисперсию по данному распределению
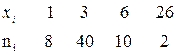
Решение. Найдем выборочную среднюю:
.
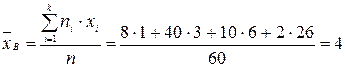Найдем среднюю квадратов значений признака:
.
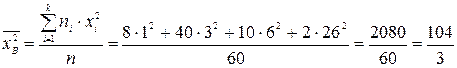Искомая дисперсия: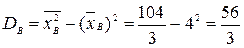 
.
Пусть нам необходимо по данным выборки оценить (приближенно найти) неизвестную генеральную дисперсию 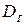. Если в качестве оценки генеральной дисперсии принять выборочную дисперсию, то эта оценка будет приводить к систематическим ошибкам, давая заниженное значение генеральной дисперсии. Объясняется это тем, что, как можно доказать, выборочная дисперсия является смещенной оценкой 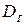другими словами, математическое ожидание выборочной дисперсии не равно оцениваемой генеральной дисперсии, а равно 
.
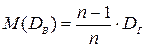Легко «исправить» выборочную дисперсию так, чтобы ее математическое ожидание было равно генеральной дисперсии. Достаточно для этого умножить 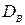на дробь 
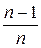. Сделав это, получим исправленную дисперсию, которую обычно обозначают через 
:
.
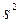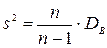Исправленная дисперсия является, конечно, несмещенной оценкой генеральной дисперсии.
Итак, в качестве оценки генеральной дисперсии принимают исправленную дисперсию .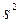
Для оценки же среднего квадратического отклонения генеральной совокупности используют «исправленное» среднее квадратическое отклонение, которое равно квадратному корню из исправленной дисперсии:
