Пусть изучается дискретная генеральная совокупность относительно количественного признака X.
Генеральной средней 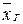 называют среднее арифметическое значений признака генеральной совокупности.
называют среднее арифметическое значений признака генеральной совокупности.
Если все значения 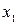 ,
, 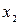 , ...,
, ..., 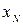 признака генеральной совокупности объема N различны, то
признака генеральной совокупности объема N различны, то 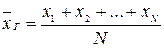 .
.
Если же значения признака 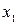 ,
, 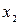 , ...,
, ..., 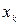 имеют соответственно частоты
имеют соответственно частоты 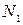 ,
, 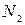 , ...,
, ..., 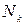 , причем
, причем 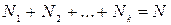 ,то
,то
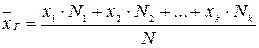 или
или 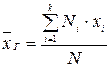 .
.
Пусть для изучения генеральной совокупности относительно количественного признака X извлечена выборка объема n.
Выборочной средней 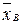 называют среднее арифметическое значение признака выборочной совокупности.
называют среднее арифметическое значение признака выборочной совокупности.
Если все значения 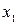 ,
, 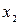 , ...,
, ..., 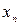 признака генеральной совокупности объема n различны, то
признака генеральной совокупности объема n различны, то 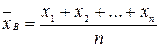 .
.
Если же значения признака 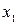 ,
, 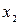 , ...,
, ..., 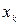 имеют соответственно частоты
имеют соответственно частоты 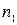 ,
, 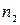 , ...,
, ..., 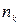 , причем
, причем 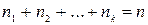 ,то
,то
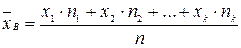 или
или 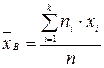 , где
, где 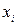 - варианта выборки,
- варианта выборки, 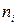 - частота варианты
- частота варианты 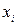 ,
, 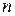 - объём выборки.
- объём выборки.
Выборочная средняя является несмещённой оценкой генеральной средней.
Пример. Из генеральной совокупности извлечена выборка:
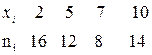
Найти несмещённую оценку генеральной средней.
Решение: Несмещённой оценкой генеральной средней является выборочная средняя 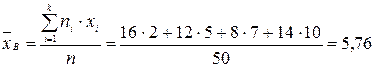
Оценка генеральной средней по выборочной средней.
Пусть из генеральной совокупности извлечена повторная выборка объема n со значениями признака  .
.
Выборочная средняя есть несмещенная оценка генеральной средней.
Выборочная средняя является состоятельной оценкой генеральной средней.

