Смысл статистических методов заключается в том, чтобы по выборке ограниченного объема 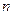 , т.е. по некоторой части генеральной совокупности, высказать обоснованное суждение об ее свойствах в целом.
, т.е. по некоторой части генеральной совокупности, высказать обоснованное суждение об ее свойствах в целом.
Числовые значения, характеризующие генеральную совокупность, называются параметрами.
Одна из задач математической статистики – определение параметров большого массива по исследованию его части.
Опр. Статистической оценкой неизвестного параметра теоретического распределения называют его приближенное значение, зависящее от данной выборки 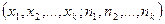 , т.е. некоторую функцию этих величин
, т.е. некоторую функцию этих величин
Здесь 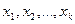 - значения признака,
- значения признака,
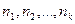 -соответствующие частоты.
-соответствующие частоты.
Статистическая оценка является случайной величиной.
Статистические оценки могут быть точечными и интервальными.
Статистическое оценивание может выполняться двумя способами:
1) точечная оценка – оценка, которая дается для некоторой определенной точки
Точечная оценка
Это оценка, которая определяется по выборке одним числом.
Обозначим через 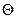 - оцениваемый параметр (им может быть и математическое ожидание и дисперсия и т.д.), а через
- оцениваемый параметр (им может быть и математическое ожидание и дисперсия и т.д.), а через 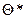 - его статистическую оценку.
- его статистическую оценку.
Опр. Величину 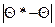 называют точностью оценки.Чем меньше
называют точностью оценки.Чем меньше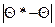 ,тем точнее определен неизвестный параметр.
,тем точнее определен неизвестный параметр.
Для того, чтобы статистические оценки давали «хорошие» приближения оцениваемых параметров, они должны удовлетворять определенным требованиям.
Чтобы оценка 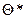 имела практическое значение, она не должна содержать систематической ошибки и иметь возможно меньшую дисперсию. Кроме того, при увеличении объема выборки вероятность сколь угодно малых отклонений
имела практическое значение, она не должна содержать систематической ошибки и иметь возможно меньшую дисперсию. Кроме того, при увеличении объема выборки вероятность сколь угодно малых отклонений 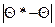 должна быть близка к 1.
должна быть близка к 1.
Опр. Оценка параметра 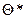 называется несмещенной, если ее математическое ожидание
называется несмещенной, если ее математическое ожидание 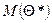 равно оцениваемому параметру
равно оцениваемому параметру 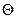 , при любом объеме выборки, т.е.
, при любом объеме выборки, т.е.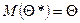 , и смещенной, если
, и смещенной, если 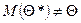 .
.
Опр. Оценка 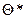 называется эффективной, если при заданном
называется эффективной, если при заданном 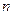 она имеет наименьшую возможную дисперсию.
она имеет наименьшую возможную дисперсию.
При рассмотрении выборок большого объема (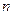 - велико) к статистическим оценкам предъявляется требованиесостоятельности.
- велико) к статистическим оценкам предъявляется требованиесостоятельности.
Опр. Оценка 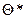 называется состоятельной, если при увеличении объема выборки она стремится по вероятности к оцениваемому параметру.
называется состоятельной, если при увеличении объема выборки она стремится по вероятности к оцениваемому параметру.
Теорема. Несмещенной, состоятельной и эффективной генеральной средней (математического ожидания) служит выборочная средняя 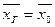 ,
, 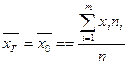 , где
, где 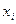 - варианта выборки,
- варианта выборки, 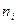 - частота встречаемой варианты
- частота встречаемой варианты 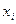 ,
, 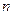 - объем выборки.
- объем выборки.
Теорема. Смещенной оценкой генеральной дисперсии служит выборочная дисперсия: 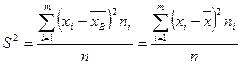 .
.
Эта оценка является смещенной, т.к.
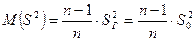 . (7)
. (7)
Теорема. Несмещенной оценкой генеральной дисперсии служит исправленная выборочная дисперсия выборочная дисперсия:
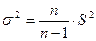 . (8)
. (8)

