Чтобы убедиться в том, что мы не допускаем чрезмерно грубой ошибки в оценке какой-то вероятностной характеристики, в теории вероятностей и математической статистике пользуются так называемыми доверительными интервалами и доверительными вероятностями.
Интервальной называют оценку, которая определяется двумя числами – концами интервала.
Допустим, что для изучения некоторой случайной величины X (признака генеральной совокупности) необходимо по статистическим данным произвести оценку неизвестного ее параметра θ (это может быть М(Х), D(Х) или р) с определенной степенью точности и надежности, т. е. надо указать границы, в которых практически достоверно лежит этот неизвестный параметр θ.
Это означает, что надо найти такую выборочную оценку для искомого параметра θ, при которой с наибольшей вероятностью (надежностью) будет выполняться неравенство:
Отсюда видно, что чем меньше e, тем точнее характеризуется неизвестный параметр θ с помощью выборочной оценки . Следовательно, число e характеризует точность оценки параметра θ.
Надежность выполнения неравенства оценивается числом g (α = 1 – γ), которое называют доверительной вероятностью:
g = Р(
).
Итак, число e характеризует точность оценки параметра θ; число g – характеризует надежность оценки параметра θ.
Доверительным называется интервал, который с заданной надежностью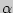 
покрывает оцениваемый параметр.
Для оценки математического ожидания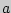 
случайной величины Х, распределенной по нормальному закону, при известном среднем квадратическом отклонении 
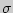служит доверительный интервал
