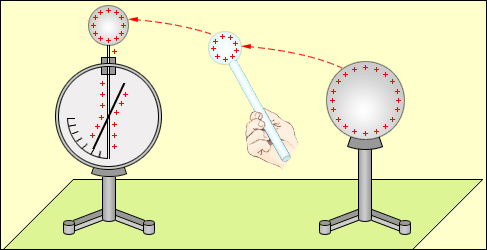
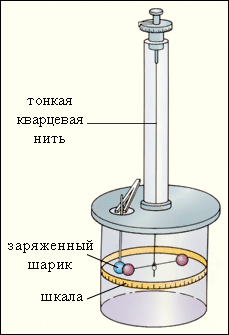
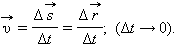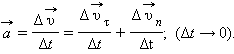Кинематикой называют раздел механики, в котором движение тел рассматривается без выяснения причин этого движения. Механическим движением тела называют изменение его положения в пространстве относительно других тел с течением времени. Движение одного и того же тела относительно разных тел оказывается различным. Для описания движения тела нужно указать, по отношению к какому телу рассматривается движение. Это тело называют телом отсчета. Система координат, связанная с телом отсчета, и часы для отсчета времени образуют систему отсчета, позволяющую определять положение движущегося тела в любой момент времени. В Международной системе единиц (СИ) за единицу длины принят метр, а за единицу времени – секунда. Всякое тело имеет определенные размеры. Различные части тела находятся в разных местах пространства. Однако, во многих задачах механики нет необходимости указывать положения отдельных частей тела. Если размеры тела малы по сравнению с расстояниями до других тел, то данное тело можно считать его материальной точкой. Так можно поступать, например, при изучении движения планет вокруг Солнца. Если все части тела движутся одинаково, то такое движение называется поступательным. Поступательно движутся, например, кабины в аттракционе «Гигантское колесо», автомобиль на прямолинейном участке пути и т. д. При поступательном движении тела его также можно рассматривать как материальную точку. Тело, размерами которого в данных условиях можно пренебречь, называется материальной точкой. Понятие материальной точки играет важную роль в механике. Перемещаясь с течением времени из одной точки в другую, тело (материальная точка) описывает некоторую линию, которую называют траекторией движения тела. Положение материальной точки в пространстве в любой момент времени (закон движения) можно определять либо с помощью зависимости координат от времени x = x(t), y = y(t), z = z(t) (координатный способ), либо при помощи зависимости от времени радиус-вектора 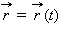 (векторный способ), проведенного из начала координат до данной точки (рис. 1.1.1).
(векторный способ), проведенного из начала координат до данной точки (рис. 1.1.1).
|
|
| Рисунок 1.1.1.
Определение положения точки с помощью координат x = x(t), y = y(t) иz = z(t) и радиус–вектора
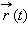 . .  – радиус–вектор положения точки в начальный момент времени. – радиус–вектор положения точки в начальный момент времени. |
Перемещением тела 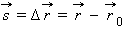 называют направленный отрезок прямой, соединяющий начальное положение тела с его последующим положением. Перемещение есть векторная величина. Пройденный путь l равен длине дуги траектории, пройденной телом за некоторое время t. Путь – скалярная величина.Если движение тела рассматривать в течение достаточно короткого промежутка времени, то вектор перемещения окажется направленным по касательной к траектории в данной точке, а его длина будет равна пройденному пути. В случае достаточно малого промежутка времени Δt пройденный телом путь Δlпочти совпадает с модулем вектора перемещения
называют направленный отрезок прямой, соединяющий начальное положение тела с его последующим положением. Перемещение есть векторная величина. Пройденный путь l равен длине дуги траектории, пройденной телом за некоторое время t. Путь – скалярная величина.Если движение тела рассматривать в течение достаточно короткого промежутка времени, то вектор перемещения окажется направленным по касательной к траектории в данной точке, а его длина будет равна пройденному пути. В случае достаточно малого промежутка времени Δt пройденный телом путь Δlпочти совпадает с модулем вектора перемещения 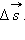 При движении тела по криволинейной траектории модуль вектора перемещения всегда меньше пройденного пути (рис. 1.1.2).
При движении тела по криволинейной траектории модуль вектора перемещения всегда меньше пройденного пути (рис. 1.1.2).
|
|
| Рисунок 1.1.2.
Пройденный путь l и векторперемещения
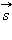 при криволинейномдвижении тела. a и b – начальная и конечная точки пути. при криволинейномдвижении тела. a и b – начальная и конечная точки пути. |
Для характеристики движения вводится понятие средней скорости:
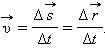 |
В физике наибольший интерес представляет не средняя, а мгновенная скорость, которая определяется как предел, к которому стремится средняя скорость за бесконечно малый промежуток времени Δt:
|
В математике такой предел называют производной и обозначают 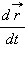 или
или  Мгновенная скорость
Мгновенная скорость 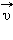 тела в любой точке криволинейной траектории направлена по касательной к траектории в этой точке. Различие между средней и мгновенной скоростями показано на рис. 1.1.3.
тела в любой точке криволинейной траектории направлена по касательной к траектории в этой точке. Различие между средней и мгновенной скоростями показано на рис. 1.1.3.
|
|
| Рисунок 1.1.3.
Средняя и мгновенная скорости.
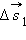 , , 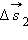 , ,  – перемещения за времена – перемещения за времена 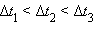 соответственно. Приt → 0 соответственно. Приt → 0 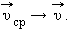 |
При движении тела по криволинейной траектории его скорость 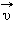 изменяется по модулю и направлению. Изменение вектора скорости
изменяется по модулю и направлению. Изменение вектора скорости 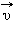 за некоторый малый промежуток времени Δt можно задать с помощью вектора
за некоторый малый промежуток времени Δt можно задать с помощью вектора 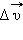 (рис. 1.1.4). Вектор изменения скорости
(рис. 1.1.4). Вектор изменения скорости  за малое время Δt можно разложить на две составляющие:
за малое время Δt можно разложить на две составляющие: 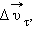 направленную вдоль вектора
направленную вдоль вектора 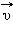 (касательная составляющая), и
(касательная составляющая), и 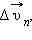 направленную перпендикулярно вектору
направленную перпендикулярно вектору 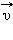 (нормальная составляющая).
(нормальная составляющая).
|
|
| Рисунок 1.1.4.
Изменение вектора скорости по величине и направлению.
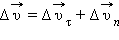 – изменение вектора скорости за время – изменение вектора скорости за время 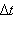 . . |
Мгновенным ускорением (или просто ускорением) 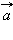 тела называют предел отношения малого изменения скорости
тела называют предел отношения малого изменения скорости 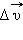 к малому промежутку времени Δt, в течение которого происходило изменение скорости:
к малому промежутку времени Δt, в течение которого происходило изменение скорости:
|
Направление вектора ускорения 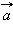 в случае криволинейного движения не совпадает с направлением вектора скорости
в случае криволинейного движения не совпадает с направлением вектора скорости 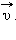 Составляющие вектора ускорения
Составляющие вектора ускорения 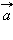 называют касательным (тангенциальным)
называют касательным (тангенциальным) 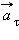 инормальным
инормальным 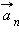 ускорениями (рис. 1.1.5).
ускорениями (рис. 1.1.5).
|
|
| Рисунок 1.1.5.
Касательное и нормальное ускорения.
|
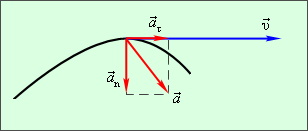
Касательное ускорение указывает, насколько быстро изменяется скорость тела по модулю:
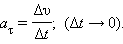 |
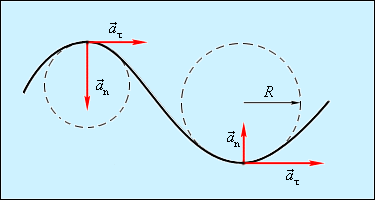
Вектор 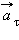 направлен по касательной к траектории. Нормальное ускорение указывает, насколько быстро скорость тела изменяется по направлению. Криволинейное движение можно представить как движение по дугам окружностей (рис. 1.1.6).
направлен по касательной к траектории. Нормальное ускорение указывает, насколько быстро скорость тела изменяется по направлению. Криволинейное движение можно представить как движение по дугам окружностей (рис. 1.1.6).
|
|
| Рисунок 1.1.6.
Движение по дугам окружностей.
|
Нормальное ускорение зависит от модуля скорости υ и от радиуса R окружности, по дуге которой тело движется в данный момент:
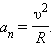 |
Вектор 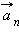 всегда направлен к центру окружности. Из рис. 1.1.5 видно, что модуль полного ускорения равен
всегда направлен к центру окружности. Из рис. 1.1.5 видно, что модуль полного ускорения равен
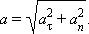 |
Таким образом, основными физическими величинами в кинематике материальной точки являются пройденный путь l, перемещение 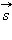 , скорость
, скорость 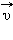 и ускорение
и ускорение 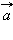 . Путь l является скалярной величиной. Перемещение
. Путь l является скалярной величиной. Перемещение 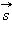 , скорость
, скорость 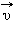 и ускорение
и ускорение 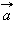 – величины векторные. Чтобы задать векторную величину, нужно задать ее модуль и указать направление. Векторные величины подчиняются определенным математическим правилам. Вектора можно проектировать на координатные оси, их можно складывать, вычитать и т. д.
– величины векторные. Чтобы задать векторную величину, нужно задать ее модуль и указать направление. Векторные величины подчиняются определенным математическим правилам. Вектора можно проектировать на координатные оси, их можно складывать, вычитать и т. д.