Стоячие волны

Стоя́чая волна́ — колебания в распределённых колебательных системах с характерным расположением чередующихся максимумов (пучностей) и минимумов (узлов) амплитуды. Практически такая волна возникает при отражениях от преград и неоднородностей в результате наложения отражённой волны на падающую. При этом крайне важное значение имеет частота, фаза и коэффициент затухания волны в месте отражения.

В случае гармонических колебаний в одномерной среде стоячая волна описывается формулой:

$u = u_0 \cos kx \cos(\omega t - \varphi)$ ,

где u — возмущения в точке х в момент времени t, $u_0$ — амплитуда стоячей волны, $\omega$ — частота , k — волновой вектор, $\varphi$ — фаза.

Стоячие волны являются решениями волновых уравнений. Их можно представить себе как суперпозицию волн, распространяющихся в противоположных направлениях.

Рассмотрим падающую и отраженную волны в виде:

$y_1\; =\; y_0\, \sin(kx - \omega t)$

$y_2\; =\; y_0\, \sin(kx + \omega t)$

где:

y0 — амплитуда волны,
$\omega$ — циклическая (угловая) частота, измеряемая в радианах в секунду,
k — волновой вектор, измеряется в радианах на метр, и рассчитывается как 2 $\pi$ поделённое на длину волны $\lambda$ ,
x и t — переменные для обозначения длины и времени.

Поэтому результирующее уравнение для стоячей волны y будет в виде суммы y1 и y2:

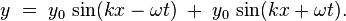
$y\; =\; y_0\, \sin(kx - \omega t)\; +\; y_0\, \sin(kx + \omega t).$

Используя тригонометрические соотношения, это уравнение можно переписать в виде:

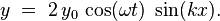
$y\; =\; 2\, y_0\, \cos(\omega t)\; \sin(kx).$

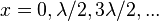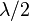Если рассматривать моды $x = 0, \lambda /2, 3\lambda /2,...$ и антимоды $x = \lambda /4, 3\lambda /4, 5\lambda /4,...$ , то расстояние между соседними модами / антимодами будет равно половине длины волны $\lambda /2$ .