Пусть координатные оси двух инерциальных систем отсчёта  и
и  параллельны друг другу,
параллельны друг другу,  — время и координаты некоторого события, наблюдаемого относительно системы
— время и координаты некоторого события, наблюдаемого относительно системы  , а
, а 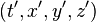 — время и координаты того же события относительно системы
— время и координаты того же события относительно системы  .
.
Общий вид преобразований Лоренца в векторном виде[13], когда скорость систем отсчёта имеет произвольное направление:

где 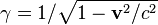 — фактор Лоренца,
— фактор Лоренца,  и
и  — радиус-векторы события относительно систем S и S'.
— радиус-векторы события относительно систем S и S'.
Если сориентировать координатные оси по направлению относительного движения инерциальных систем (то есть в общие формулы подставить  ) и выбрать это направление в качестве оси
) и выбрать это направление в качестве оси  (то есть так, чтобы система S' двигалась равномерно и прямолинейно со скоростью
(то есть так, чтобы система S' двигалась равномерно и прямолинейно со скоростью  относительно S вдоль оси
относительно S вдоль оси  ), то преобразования Лоренца примут следующий вид:
), то преобразования Лоренца примут следующий вид:

где  — скорость света. При скоростях много меньше скорости света (
— скорость света. При скоростях много меньше скорости света (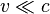 ) преобразования Лоренца переходят в преобразования Галилея:
) преобразования Лоренца переходят в преобразования Галилея:

Подобный предельный переход является отражением принципа соответствия, согласно которому более общая теория (СТО) имеет своим предельным случаем менее общую теорию (в данном случае — классическую механику).

