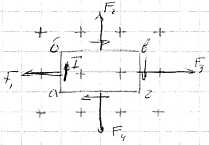
Предположим, что контур перемещается слева на право, тогда работа, совершенная силами “F2” и “F4” будут равны.
Т.к. контур перемещается слева на право, то “F3 > F1”;
F = F3 – F1
Ф2 = Ф1 + ∆Ф;
Ф1 – в начале перемещения;
Ф2 – в конце перемещения
Сторона “аб” совершает отрицательную работу “Aаб = -I·Ф”; “бв” и “аг” не совершают работы, т.к. силы “F2” и “F4” направлены под углом 90º к перемещению.
Если контур перемещается под действием сил поля, то изменение потока “∆Ф” будет всегда положительным.
Ф2 > Ф1; ∆Ф > 0
Всякий контур с током находящийся в магнитном поле, под действием электромагнитных сил, занимает всегда такое положение при котором “Ф” проницаемости контура будет максимальным и положительным.
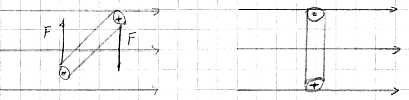
Магни́тный моме́нт, магни́тный дипо́льный моме́нт — основная величина, характеризующая магнитные свойства вещества (источником магнетизма, согласно классической теории электромагнитных явлений, являются электрические макро- и микротоки; элементарным источником магнетизма считают замкнутый ток). Магнитным моментом обладают элементарные частицы, атомные ядра, электронные оболочки атомв и молекул. Магнитный момент элементарных частиц (электронов, протонов, нейтронов и других), как показала квантовая механика, обусловлен существованием у них собственного механического момента — спина.
В случае плоского контура с электрическим током магнитный момент вычисляется как
В случае плоского контура с электрическим током магнитный момент вычисляется как
 ,
,
где  — сила тока в контуре,
— сила тока в контуре,  — площадь контура,
— площадь контура, 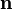 — единичный вектор нормали к плоскости контура. Направление магнитного момента обычно находится по правилу буравчика если вращать ручку буравчика в направлении тока, то направление магнитного момента будет совпадать с направлением поступательного движения буравчика.
— единичный вектор нормали к плоскости контура. Направление магнитного момента обычно находится по правилу буравчика если вращать ручку буравчика в направлении тока, то направление магнитного момента будет совпадать с направлением поступательного движения буравчика.
Для произвольного замкнутого контура магнитный момент находится из:
![\mathbf{m} = {I \over 2}\oint[\mathbf{r}, d\mathbf{l}]](http://upload.wikimedia.org/math/9/b/c/9bc3e21d4acf8d72e24488bc2eb5fc62.png) ,
,
где  — радиус-вектор, проведенный из начала координат до элемента длины контура
— радиус-вектор, проведенный из начала координат до элемента длины контура 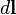
В общем случае произвольного распределения токов в среде:
![\mathbf{m} = {1 \over 2}\int\limits_{V}[\mathbf{r}, \mathbf{j}]dV](http://upload.wikimedia.org/math/a/0/7/a07a4eb227ee65896c4cf66ac43d7622.png) ,
,
где 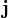 — плотность тока в элементе объёма
— плотность тока в элементе объёма 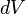 .
.

