Затухающие колебания.

Пусть имеется система, состоящая из пружины (подчиняющейся закону Гука), один конец которой жёстко закреплён, а на другом находится тело массой m. Колебания совершаются в среде, где сила сопротивления пропорциональна скорости с коэффициентом c

Тогда второй закон Ньютона для рассматриваемой системы запишется так:

$m \vec{a} = \vec{F_c} + \vec{F_y}$

где $F_c$ — сила сопротивления, $F_y$ — сила упругости

$F_c = -cv$ , $F_y = -kx$ , то есть

$m a + c v + k x = 0$

или в дифференциальной форме

$\ddot{x} + { c \over m} \dot{x} + {k \over m} x = 0$

где k — коэффициент упругости в законе Гука, c — коэффициент сопротивления, устанавливающий соотношение между скоростью движения грузика и возникающей при этом силой сопротивления.

Для упрощения вводятся следующие обозначения: $\omega_0 = \sqrt{ k \over m },\qquad \zeta = { c \over 2 \sqrt{k m} }.$

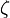Величину $\omega_0$ называют собственной частотой системы, $\zeta$ — коэффициентом затухания.

Тогда дифференциальное уравнение принимает вид

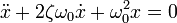
$\ddot{x} + 2 \zeta \omega_0 \dot{x} + \omega_0^2 x = 0$

Сделав замену $x = e^{\lambda t}$ , получают характеристическое уравнение

$\lambda^2 + 2 \zeta \omega_0 \lambda + \omega_0^2 = 0$

Корни которого вычисляются по следующей формуле

$\lambda_\pm = \omega_0( - \zeta \pm \sqrt{\zeta^2 - 1})$