Матрицей называется прямоугольная таблица из чисел, содержащая некоторое количество m строк и некоторое количество n столбцов.
Виды матриц:
1.Матрица размера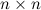 
называется квадратной, число 
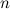называется порядком матрицы.
2. Квадратная матрица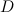 
называется диагональной, если все ее элементы, стоящие вне главной диагонали, равны нулю.
3.Единичной матрицей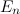 
называется скалярная матрица порядка 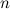, диагональные элементы которой равны 1.
4.Матрица называется верхней треугольной матрицей, если все элементы ниже главной диагонали равны нулю.
Матрица называется нижней треугольной матрицей, если все элементы выше главной диагонали равны нулю.
5.Ступенчатой называется матрица, удовлетворяющая следующим условиям:
если эта матрица содержит нулевую строку (т.е. строку, все элементы которой равны нулю), то все строки, расположенные под нею, также нулевые;
если первый ненулевой элемент некоторой строки расположен в столбце с номером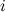 
, то первый ненулевой элемент следующей строки должен находиться в столбце с номером большим, чем .
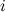Элементарные преобразования матрицы — это такие преобразования матрицы, в результате которых сохраняется эквивалентность матриц. Таким образом, элементарные преобразования не изменяют множество решений системы линейных алгебраических уравнений, которую представляет эта матрица.
Элементарные преобразования используются в методе Гаусса для приведения матрицы к треугольному или ступенчатому виду.
