Событие “n испытаний привели m раз к успеху” содержит столько элементарных событий, сколькими способами можно распределить m символов по n местам, что совпадает с числом сочетаний 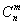 из n элементов по m.
из n элементов по m.
Другими словами, пространство элементарных событий состоит из 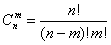 точек, каждая из которых, по определению, имеет вероятность
точек, каждая из которых, по определению, имеет вероятность 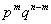 .
.
Следовательно, вероятность m успехов (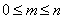 ) в серии из n испытаний Бернулли описывается формулой
) в серии из n испытаний Бернулли описывается формулой
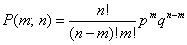 , (*)
, (*)
где p – вероятность успеха; q – вероятность неудачи в одном испытании (q = 1 – р).
Согласно существующей терминологии, число успехов в серии из n испытаний является случайной величиной, а формула (*) описывает распределение этой случайной величины и называется биномиальным законом распределения вероятности.
Заметим, что выражение 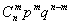 представляет собой m-ый член биномиального разложения
представляет собой m-ый член биномиального разложения 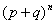 .
.
Следовательно,
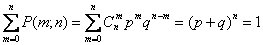 ,
,
как того и требует понятие вероятности.
Выражение, содержащее произведение вида 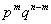 , представляет собой вероятность m успехов в серии из n испытаний Бернулли:
, представляет собой вероятность m успехов в серии из n испытаний Бернулли:
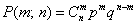 .
.
Заметим, что события
– 0 успехов,
– 1 успех,
– 2 успеха,
– …,
– n успехов в серии из n испытаний Бернулли
образуют полную группу событий, поскольку они попарно несовместимы и вместе образуют достоверное событие.
Частные случаи.
– Вероятность того, что в серии из n испытаний успех не наступит ни разу, равна 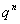 .
.
– Вероятность наступления хотя бы одного успеха в серии из n испытаний равна
 (**)
(**)
1.4. Сложение и умножение вероятностей
Событие А называется частным случаем события В, если при наступлении А наступает и В. То, что А является частным случаем В, записываем  .
.
События А и В называются равными, если каждое из них является частным случаем другого. Равенство событий А и В записываем А = В.
Суммой событий А и В называется событие А + В, которое наступает тогда и только тогда, когда наступает хотя бы одно из событий: А или В.
Теорема о сложении вероятностей. Вероятность появления одного из двух несовместныхсобытий равна сумме вероятностей этих событий.

Заметим, что сформулированная теорема справедлива для любого числа несовместных событий:
 .
.
Если случайные события  образуют полную группу несовместных событий, то имеет место равенство
образуют полную группу несовместных событий, то имеет место равенство
 .
.
Произведением событий А и В называется событие АВ, которое наступает тогда и только тогда, когда наступают оба события: А и В одновременно. Случайные события А и B называютсясовместными, если при данном испытании могут произойти оба эти события.
Теорема о сложении вероятностей 2. Вероятность суммы совместных событий вычисляется по формуле
 .
.
События событий А и В называются независимыми, если появление одного из них не меняет вероятности появления другого. Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет.
Теорема об умножении вероятностей. Вероятность произведения независимых событий А и Ввычисляется по формуле:
 .
.

