Метод последовательных приближений

Метод последовательных приближений применяется для уравнений Фредгольма 2-го рода, если выполняется условие:

$|\lambda||b-a|\max_{a\leqslant x,\;s\leqslant b}|K(x,\;s)|<1.$

Это условие необходимо для сходимости ряда Лиувилля — Неймана:

$\varphi(x)=\sum_{k=0}^\infty\lambda^k(K^kf)(x),$

который и является решением уравнения. $(K^kf)(x)$ — $k$ -ая степень интегрального оператора $(Kf)(x)$ :

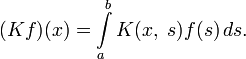
$(Kf)(x)=\int\limits_a^b K(x,\;s)f(s)\,ds.$

Впрочем, такое решение является хорошим приближением лишь при достаточно малых $|\lambda|$ .

Этот метод применим также и при решении уравнений Вольтерры 2-го рода. В таком случае, ряд Лиувилля - Неймана сходится при любых значениях $|\lambda|$ , а не только при малых.