Признак Даламбера
Пусть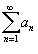 
− ряд с положительными членами. Тогда справедливы следующие свойства:
- Если
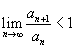, то ряд 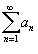сходится; - Если
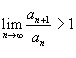, то ряд 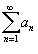расходится; - Если
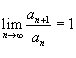, то ряд 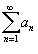может как сходиться, так и расходиться. В этом случае для установления сходимости нужно использовать другие признаки.
Радикальный признак Коши
Снова рассмотрим ряд 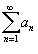с положительными членами. Согласно признаку Коши:
- Если
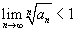, то ряд 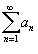сходится; - Если
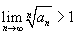, то ряд 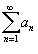расходится; - Если
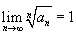, то вопрос о сходимости ряда 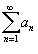, также как для признака Даламбера, остается открытым.
