Признаки сравнения рядов
Даны два ряда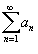 
и 
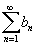− такие, что 
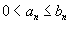для всех n. Тогда справедливы следующие признаки:
- Если 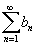сходится, то 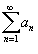также сходится;
- Если 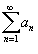расходится, то 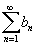также расходится.
Предельные признаки сравнения рядов
Пусть даны два ряда 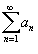и 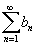, у которых члены an и bn положительны для всех n. Тогда справедливы следующие предельные признаки:
- Если
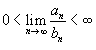, то оба ряда 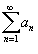и 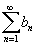либо сходятся, либо расходятся; - Если
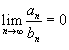, то ряд 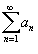сходится, если сходится ряд 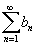; - Если
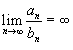, то ряд 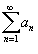расходится, если расходится ряд .
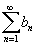Так называемый обобщенный гармонический ряд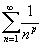 
сходится при p > 1 и расходится при 0 < p ≤ 1.
