Определение:
Простыми дробями называются рациональные дроби вида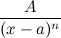 
, 
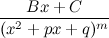, где 
,
.
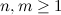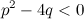Теорема:
(О разложении многочлена на элементарные множители)
Многочлен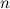 
-ой степени может быть разложен на произведение сомножителей следующим образом:
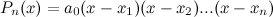
Здесь 
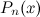- корни многочлена 
, а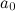 
- коэффициент при старшей степени 
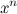указанного многочлена.
Квадратный трехчлен можно разложить на множители следующим образом:
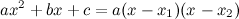
если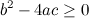 
. Здесь 
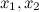- корни многочлена 
.
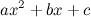Определение:
Рациональная дробь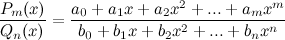 
называется правильной, если степень многочлена числителя меньше степени многочлена знаменателя, т.е. 
.
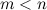