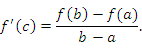Теорема.
Пусть функция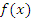 
дифференцируема в открытом промежутке 
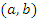и сохраняет непрерывность на концах этого промежутка. Тогда существует такая точка 
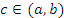, что
|
|
Доказательство.
Рассмотрим вспомогательную функцию
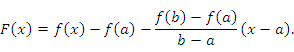
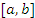, а на его концах принимает одинаковые значения:
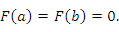
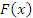удовлетворяет всем условиям теоремы Ролля и, следовательно, существует точка 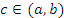, в которой производная функции 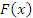равна нулю:
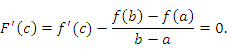
Следствие 1.
В частном случае, когда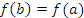 
, из теоремы Лагранжа вытекает, что существует точка 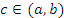, в которой производная функции 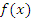равна нулю: 
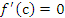. Это означает, что теорема Лагранжа является обобщением теоремы Ролля.
Следствие 2.
Если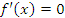 
во всех точках некоторого промежутка 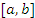, то 
в этом промежутке.
Действительно, пусть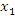 
и 
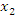– произвольные точки промежутка 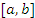и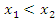 
. Применяя теорему Лагранжа к промежутку 
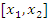, получим
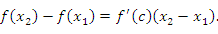
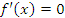во всех точках промежутка 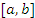. Тогда
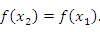
Учитывая произвольность точек и , получаем требуемое утверждение.
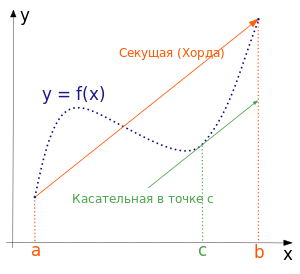
. То есть существует такая точка c, что касательная к графику в этой точке параллальна хорде.
