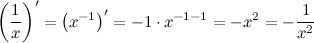Определение. Пусть функция y=f(x) непрерывна и строго монотонна в некоторой окрестности точки x0, и пусть в этой точке существует производная f′(x0)≠0.Тогда обратная функция в точке y0=f(x0) имеет производную, которая может быть найдена по форумуле (f−1(y0))′=1f′(x0).
Формула:
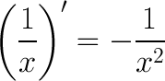
Известно свойство степеней, что
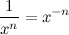
тогда
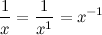
Используя производную степенной функции:
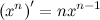
будем иметь: