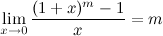Предел последовательности 
обозначается буквой e:
.Число e является иррациональным и приблизительно равно 
. Это число принято за основание логарифмов, которые называют натуральными логарифмами и обозначают lnx (lnx=logex).
Формула выполняется и для функций:
. Это число принято за основание логарифмов, которые называют натуральными логарифмами и обозначают lnx (lnx=logex). Формула выполняется и для функций:
Предел (5) называется вторым замечательным пределом. Критерий для его распознавания включает в себя три требования:
1) должна быть неопределенность вида 1∞,
2) 1+бесконечно малая, или короче: 1+б.м.,
3)
, причем в показателе степени стоит не произвольная бесконечно большая, а величина, обратная той бесконечно малой, которая прибавляется к числу 1.
Так, среди пределов
, 
, 
, 
только второй и третий равны 
.
1) должна быть неопределенность вида 1∞,
2) 1+бесконечно малая, или короче: 1+б.м.,
3)
, причем в показателе степени стоит не произвольная бесконечно большая, а величина, обратная той бесконечно малой, которая прибавляется к числу 1. Так, среди пределов
, , , только второй и третий равны .Следствия из второго замечательного предела:
1°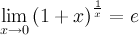 
2°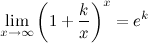 
3°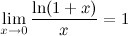 
4°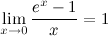 
5°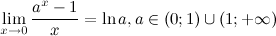 
6° 
