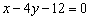Общее уравнение плоскости в декартовой системе координат записывается следующим образом:
| ax + by + cz + d = 0. |
Если известно, что плоскость проходит через точку с координатами (x0, y0, z0), то ее уравнение можно привести к виду
| a (x – x0) + b (y – y0) + c (z – z0) = 0. |
Уравнение:
 |
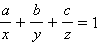называется уравнением плоскости в отрезках на осях.
Нормаль к плоскости имеет координаты
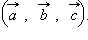
Угол между двумя плоскостями легко вычисляется по формуле скалярного произведения. Если эти плоскости задаются уравнениями a1x + b1y + c1z + d1 = 0 иa2x + b2y + c2z + d2 = 0, то угол между плоскостями равняется
 |
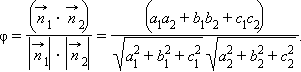Уравнение плоскости, проходящей через данную точку с данной нормалью
Уравнение плоскости, проходящей через точку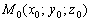 
перпендикулярно вектору 
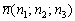, выражается формулой:
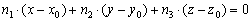
Выглядит значительно привлекательнее, чем предыдущие мытарства. В некоторых задачах аналитической геометрии уравнение плоскости можно составить несколькими способами, и решение через точку и нормальный вектор – самое оптимальное.
Пример 6
Составить уравнение плоскости по точке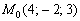 
и вектору нормали 
.
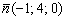Решение: Используем формулу: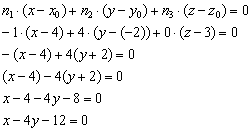
Ответ: 
