Конечные вероятностные пространства
Простым и часто используемым примером вероятностного пространства является конечное пространство. Пусть  — конечное множество, содержащее
— конечное множество, содержащее  элементов.
элементов.
В качестве сигма-алгебры удобно взять семейство подмножеств  . Его часто символически обозначают
. Его часто символически обозначают  . Легко показать, что общее число членов этого семейства, т.е. число различных случайных событий, как раз равно
. Легко показать, что общее число членов этого семейства, т.е. число различных случайных событий, как раз равно 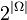 , что объясняет обозначение.
, что объясняет обозначение.
Вероятность, вообще говоря, можно определять произвольно; однако, в дискретных моделях зачастую нет причин считать, что один элементарный исход чем-либо предпочтительнее другого. В таком случае, естественным способом ввести вероятность является:
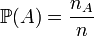 ,
,
где  , и
, и  - число элементарных исходов, принадлежащих
- число элементарных исходов, принадлежащих  . В частности, вероятность любого элементарного события:
. В частности, вероятность любого элементарного события:

Пример
Рассмотрим эксперимент с бросанием уравновешенной монеты. Естественным будет взять два события: выпадение герба ( ) и выпадение решки (
) и выпадение решки (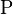 ), то есть
), то есть 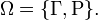 Тогда
Тогда  и вероятность можно посчитать следующим образом:
и вероятность можно посчитать следующим образом:

Таким образом определена тройка  — вероятностное пространство, в рамках которого можно рассматривать различные задачи.
— вероятностное пространство, в рамках которого можно рассматривать различные задачи.
Элементарные события
В теории вероятностей элементарные события или события-атомы — это исходы случайного эксперимента, из которых в эксперименте происходит ровно один. Множество всех элементарных событий обычно обозначается  .
.
Всякое подмножество множества  элементарных событий называется случайным событием. Говорят, что в результате эксперимента произошлослучайное событие
элементарных событий называется случайным событием. Говорят, что в результате эксперимента произошлослучайное событие  , если (элементарный) исход эксперимента является элементом
, если (элементарный) исход эксперимента является элементом  .
.
В определении вероятностного пространства на множестве случайных событий вводится сигма-аддитивная конечная мера, называемая вероятностью.
Элементарные события могут иметь вероятности, которые строго положительны, нули, неопределенны, или любая комбинация из этих вариантов. Например, любое дискретное вероятностное распределение определяется вероятностями того, что может быть названо элементарными событиями. Напротив, все элементарные события имеют вероятность нуль для непрерывного распределения. Смешанные распределения, не будучи ни непрерывными, ни дискретными, могут содержать атомы, которые могут мыслиться как элементарные (то есть события-атомы) события с ненулевой вероятностью. В теории меры в определении вероятностного пространства вероятность произвольного элементарного события не могла быть определена до тех пор, пока математики не увидели различие между пространством исходов S и событиями, которые представляют интерес, и которые определяются как элементы σ-алгебры событий из S.
Формально говоря, элементарное событие — это подмножество пространства исходов случайного эксперимента, которое состоит только из одного элемента; то есть элементарное событие — это всё ещё множество, но не сам элемент. Однако элементарные события обычно записываются как элементы, а не как множества с целью упрощения, когда это не может вызвать недоразумения.
Примеры
Примеры пространств исходов эксперимента,  , и элементарных событий:
, и элементарных событий:
- Если объекты счётны, а пространство исходов
 (натуральные числа), то элементарные события — это любые множества
(натуральные числа), то элементарные события — это любые множества 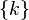 , где
, где  .
. - Если монета бросается дважды,
 ,
,  для орла, а
для орла, а  для решки, то элементарные события:
для решки, то элементарные события:  ,
,  ,
, 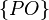 и
и  .
. - Если
 — это нормально распределенные случайные величины,
— это нормально распределенные случайные величины,  , реальные числа, то элементарные события — любые множества
, реальные числа, то элементарные события — любые множества 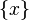 , где
, где  . Этот пример показывает, что непрерывное вероятностное распределение не определяется вероятностями событий-атомов, поскольку здесь вероятности всех элементарных событий равны нулю.
. Этот пример показывает, что непрерывное вероятностное распределение не определяется вероятностями событий-атомов, поскольку здесь вероятности всех элементарных событий равны нулю.

