В комбинаторике сочетанием из  по
по  называется набор
называется набор  элементов, выбранных из данного множества, содержащего
элементов, выбранных из данного множества, содержащего  различных элементов. Наборы, отличающиеся только порядком следования элементов (но не составом), считаются одинаковыми, этим сочетания отличаются от размещений.
различных элементов. Наборы, отличающиеся только порядком следования элементов (но не составом), считаются одинаковыми, этим сочетания отличаются от размещений.
Так, например, наборы (3-элементные сочетания, подмножества,  ) {2, 1, 3} и {3, 2, 1} 6-элементного множества {1, 2, 3, 4, 5, 6} (
) {2, 1, 3} и {3, 2, 1} 6-элементного множества {1, 2, 3, 4, 5, 6} ( ) являются одинаковыми (в то время как размещения были бы разными) и состоят из одних и тех же элементов {1,2,3}.
) являются одинаковыми (в то время как размещения были бы разными) и состоят из одних и тех же элементов {1,2,3}.
В общем случае число, показывающее, сколькими способами можно выбрать  элементов из множества, содержащего
элементов из множества, содержащего  различных элементов, стоит на пересечении
различных элементов, стоит на пересечении  -й диагонали и
-й диагонали и  -й строки треугольника Паскаля.[1]
-й строки треугольника Паскаля.[1]
Число сочетаний из  по
по  равно биномиальному коэффициенту
равно биномиальному коэффициенту

При фиксированном  производящей функцией последовательности чисел сочетаний
производящей функцией последовательности чисел сочетаний  ,
,  ,
, 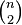 , … является:
, … является:


