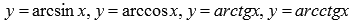1)Постоянная функция (константа), ее график и свойства.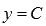 
2)Корень n-ой степени, свойства и график.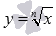 
3)Степенная функция, ее график и свойства. 
Свойства степенной функции с нечетным положительным показателем.
- Область определения:
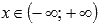. - Область значений:
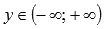. - Функция нечетная, так как
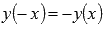. - Функция возрастает при .
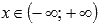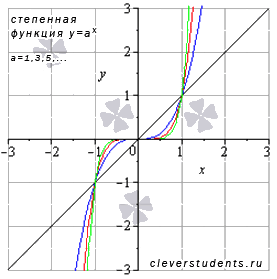
- Функция выпуклая при
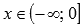и вогнутая при 
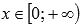(кроме линейной функции). - Точка (0;0) является точкой перегиба (кроме линейной функции).
- Асимптот нет.
- Функция проходит через точки (-1;-1), (0;0), (1;1).
Свойства степенной функции с четным положительным показателем.
- Область определения: .
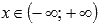- Область значений:
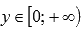. - Функция четная, так как
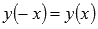. - Функция возрастает при 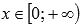, убывает при .
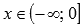- Функция вогнутая при .
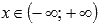- Точек перегиба нет.
- Асимптот нет.
- Функция проходит через точки (-1;1), (0;0), (1;1).
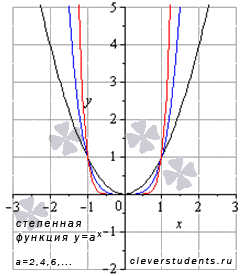
Свойства степенной функции с нечетным отрицательным показателем.
- Область определения:
.
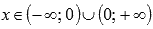При x=0 имеем разрыв второго рода, так как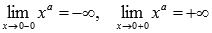
приа=-1,-3,-5,…. Следовательно, прямая x=0 является вертикальной асимптотой. - Область значений:
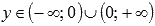. - Функция нечетная, так как .
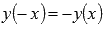- Функция убывает при .
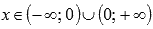- Функция выпуклая при
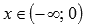и вогнутая при 
. - Точек перегиба нет.
- Горизонтальной асимптотой является прямая y = 0, так как
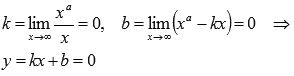
при а=-1,-3,-5,…. - Функция проходит через точки (-1;-1), (1;1).
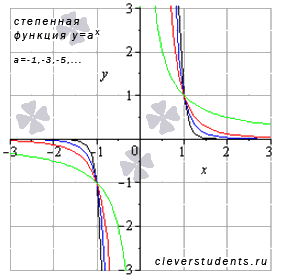
Свойства степенной функции с четным отрицательным показателем.
- Область определения: .
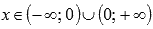При x=0 имеем разрыв второго рода, так как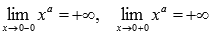
приа=-2,-4,-6,…. Следовательно, прямая x=0 является вертикальной асимптотой. - Область значений:
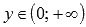. - Функция четная, так как .
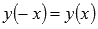- Функция возрастает при 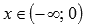, убывает при .
- Функция вогнутая при .
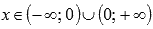- Точек перегиба нет.
- Горизонтальной асимптотой является прямая y=0, так как
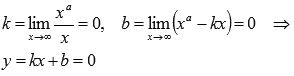
при а=-2,-4,-6,…. - Функция проходит через точки (-1;1), (1;1).
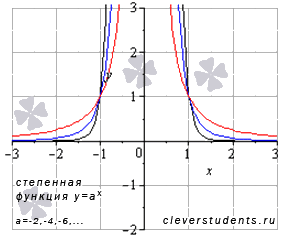
Свойства степенной функции при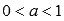 
.
- Область определения: .
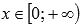- Область значений: .
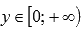- Функция не является ни четной, ни нечетной, то есть она общего вида.
- Функция возрастает при .
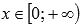- Функция выпуклая при .
- Точек перегиба нет.
- Асимптот нет.
- Функция проходит через точки (0;0), (1;1).
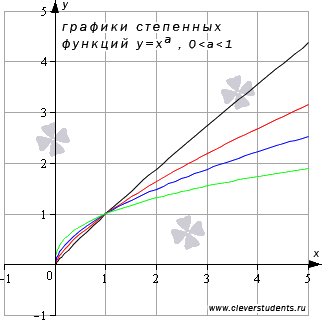
Свойства степенной функции при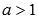 
.
- Область определения: .
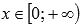- Область значений: .
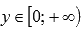- Функция не является ни четной, ни нечетной, то есть она общего вида.
- Функция возрастает при .
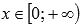- Функция вогнутая при , если
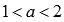; при 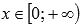, если 
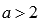. - Точек перегиба нет.
- Асимптот нет.
- Функция проходит через точки (0;0), (1;1).
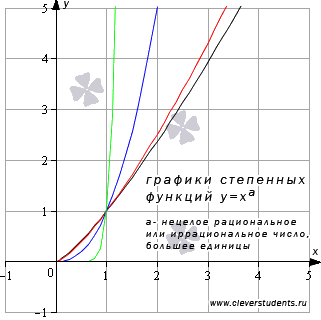
Свойства степенной функции с показателем a, 
.
- Область определения: .
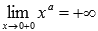при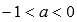 
, следовательно, х=0 является вертикальной асимптотой. - Область значений: .
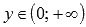- Функция не является ни четной, ни нечетной, то есть она общего вида.
- Функция убывает при .
- Функция вогнутая при .
- Точек перегиба нет.
- Горизонтальной асимптотой является прямая y=0.
- Функция проходит через точку (1;1).
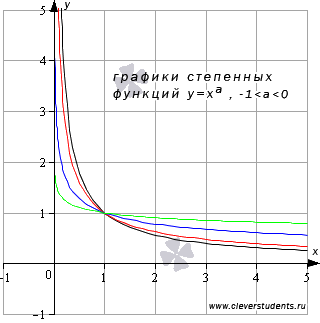
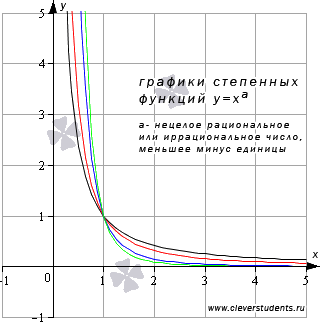
Свойства степенной функции с нецелым отрицательным показателем, меньшим минус единицы.
- Область определения: . 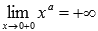при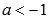
, следовательно, х=0 является вертикальной асимптотой. - Область значений: .
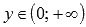- Функция не является ни четной, ни нечетной, то есть она общего вида.
- Функция убывает при .
- Функция вогнутая при .
- Точек перегиба нет.
- Горизонтальной асимптотой является прямая y=0.
- Функция проходит через точку (1;1).
4)Показательная функция, свойства, график.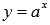 
5)Логарифмическая функция, ее свойства, графическая иллюстрация.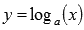 
6)Свойства и графики тригонометрических функций. 
7)Обратные тригонометрические функции (аркфункции), их свойства и графики. 
