Преобразования Галилея, закон сложения скоростей в классической механике; механический принцип относительности.

Согласно представлениям классической механики, механические явления происходят одинаково в двух системах отсчета, движущихся равномерно и прямолинейно относительно друг друга.

Рассмотрим две инерциальные системы отсчета k и k'. Система k' движется относительно k со скоростью v = const вдоль оси x. Точка М движется в двух системах отсчета (рис. 8.1).

Рис. 8.1

Прямые преобразования Галилея

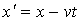
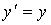
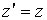
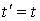
Обратные преобразования Галилиея

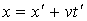
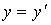
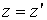
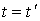
Продифференцируем это выражение по времени, получим (рис. 8.2):

или

(8.1.3)

Из преобразований Галилея и принципа относительности следует, что взаимодействия в классической физике должны передаваться с бесконечно большой скоростью c = ∞, т. к. в противном случае можно было бы одну инерциальную систему отсчета отличить от другой по характеру протекания в них физических процессов.
Рис. 8.2

Выражение (8.1.3) определяет закон сложения скоростей в классической механике. Из него следует, что скорость движения точки М (сигнала) в системе k' и в системе k различна.

Законы природы, определяющие изменение состояния движения механических систем, не зависят от того, к какой из двух инерциальных систем отсчета они относятся. Это и есть принцип относительности Галилея.