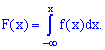Функция распределения плотности вероятностей и ее свойства.
Из формулы P{Α ≤ X < Β}=F(Β)-F(Α)следует, что вероятность попадания случайной величины в заданный интервал определяется скоростью изменения функции распределения вероятностей на этом интервале. Скорость изменения непрерывной функции равна ее производной. Это позволяет ввести новую функцию для задания случайной величины. Рассмотрим снова вероятность попадания случайной величины в интервал [x,x+Δx]:
P{x≤X<x+Δx}=F(x+Δx)-F(x).
Пусть Х - непрерывная случайная величина. Тогда для малых значений Δx эта вероятность будет также достаточно малой. Поделим ее на Δx и перейдем к пределу при Δx →0:
limΔx →0(P{x≤X<x+Δx}/Δx)=limΔx →0(F(x+Δx)-F(x))/Δx).
Если это предел существует, то он равен производной от функции распределения F(x):
limΔx →0(F(x+Δx)-F(x))/Δx)=F'(x)=f(x).
Функция f(x) называется плотностью распределения вероятностей случайной величины Х. Из определения следует, что при малых значениях Δx справедливо равенство:
P{x≤X<x+Δx}≈f(x)*Δx
Свойства плотности вероятностей
1. Плотность вероятностей принимает положительные значения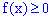 
. Это свойство следует из определения первой производной от функции распределения 
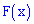, которая в свою очередь является неубывающей функцией.
2. Условие нормирования случайной величины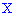 
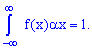
3.Вероятность попадания случайной величины в промежуток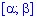 
определяется зависимостью
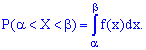
4. Функция распределения вероятностей непрерывной случайной величины определяется через плотность распределения вероятностей интегрированием
