Классическое определение вероятности. Свойства вероятности.

Вероятность события А называется отношение числа благоприятных событию А исходов к общему числу всех равновозможных несовместимых исходов. образующих полную группу Р(А)=m/n.

m- число благоприятных А исходов

n-общее число всех исходов.

Следствие 1: Вероятность невозможных событий = 0, т.е. m=0

Следствие 2: Вероятность достоверного события =1

Следствие 3: вероятность случайного события 0<Р<1, т.к. m<n

Вывод: Вероятность всегда находится 0<=Р<=1

Свойства вероятности.

1) вероятность невозможного события (пустого множества $\varnothing$ ) равна нулю:

$\mathbf{P}\{\varnothing\}=0;$

Это следует из того, что каждое событие можно представить как сумму этого события и невозможного события, что в силу аддитивности и конечности вероятностной меры означает, что вероятность невозможного события должна быть равна нулю.

2) если событие A «входит» в событие B, то есть 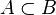$A \subset B$ , то есть наступление события A влечёт также наступление события B, то:

$\mathbf{P}\{A\}\leqslant\mathbf{P}\{B\};$

Это следует из неотрицательности и аддитивности вероятностной меры, так как событие $B$ , возможно, «содержит» кроме события $A$ ещё какие-то другие события, несовместные с $A$ .

3) вероятность каждого события $A$ находится от 0 до 1, то есть удовлетворяет неравенствам:

$0\leqslant\mathbf{P}\{A\}\leqslant1;$

Первая часть неравенства (неотрицательность) утверждается аксиоматически, а вторая следует из предыдущего свойства с учётом того, что любое событие «входит» в $X$ , а для $X$ аксиоматически предполагается $\mathbf{P}\{X\}=1$ .

4) вероятность наступления события $B\setminus A$ , заключающегося в наступлении события $B$ при одновременном ненаступлении события $A$ , равна:

$\mathbf{P}\{B\setminus A\}=\mathbf{P}\{B\}-\mathbf{P}\{A\};$

Это следует из аддитивности вероятности для несовместных событий и из того, что события $A$ и $B \setminus A$ являются несовместными по определению, а их сумма равна событию $B$ .

5) вероятность события $\bar{A}$ , противоположного событию $A$ , равна:

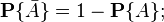
$\mathbf{P}\{\bar{A}\}=1-\mathbf{P}\{A\};$

Это следует из предыдущего свойства, если в качестве множества $B$ использовать всё пространство $X$ и учесть, что $\mathbf{P}\{X\}=1$ .

6) (теорема сложения вероятностей) вероятность наступления хотя бы одного из (то есть суммы) произвольных (не обязательно несовместных) двух событий $A$ и $B$ равна:

$\mathbf{P}\{A+B\}=\mathbf{P}\{A\}+\mathbf{P}\{B\}-\mathbf{P}\{AB\}.$

Это свойство можно получить, если представить объединение двух произвольных множеств как объединение двух непересекающихся — первого и разности между вторым и пересечением исходных множеств: $A+B=A+(B \setminus (AB))$ . Отсюда учитывая аддитивность вероятности для непересекающихся множеств и формулу для вероятности разности (см. свойство 4) множеств, получаем требуемое свойство.