Статистическая значимость множественной регрессии в целом, так же как и в парной регрессии, оценивается с помощью F-критерия Фишера:
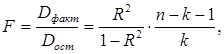 (1.30)
(1.30)
где Dфакт. - факторная сумма квадратов на одну степень свободы;
Dост. -остаточная сумма квадратов на одну степень свободы;
R2 - коэффициент (индекс) множественной детерминации;
k - число параметров при переменных х ;
n - число наблюдений.
Фактическое значение F – критерия сравнивается с табличным при 5 % - ном уровне значимости и числе степеней свободы: k иn-k-1. Если фактическая величина критерия Фишера больше его табличного значения, то построенная многофакторная модель признается статистически значимой.
Частный F – критерий оценивает статистическую значимость присутствия каждого фактора в уравнении или, другими словами, оценивает целесообразность включения фактора в модель. В общем виде для фактора хi частный F – критерий определится как
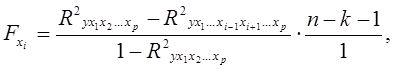 (1.31)
(1.31)
где R2 yx1x2…xp- множественный коэффициент детерминации всего комплекса р факторов с результатом;
R2 yx1x2…xi-1 xi+1…xp - тот же показатель детерминации, но без включения в модель фактора xi.
Фактическое значениечастного F – критерия сравнивается с табличным при 5 % - ном уровне значимости и числе степеней свободы: 1 и n-k-1. Если фактическое значение частного критерия Фишера Fxi превышает табличное, то дополнительное включение фактора xi в модель статистически оправданно.
Для двухфакторной модели оценка целесообразности включения одного фактора после другого осуществляется по формулам:
- фактора х1 после фактора х2:
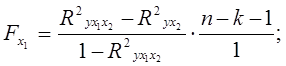 (1.32)
(1.32)
- фактора х2 после фактора х1:
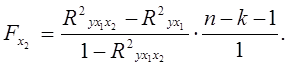 (1.33)
(1.33)
Оценка статистической значимости коэффициентов чистой регрессии производится с помощью t - критерия Стьюдента по формулам:
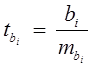 или
или 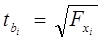 . (1.34)
. (1.34)
mbi- стандартная ошибка коэффициента регрессии bi, она может быть определена по формуле:
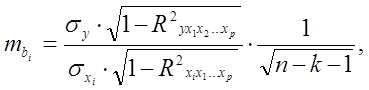 (1.35)
(1.35)
где 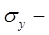 среднее квадратическое отклонение для признака у;
среднее квадратическое отклонение для признака у;
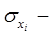 среднее квадратическое отклонение для признака xi;
среднее квадратическое отклонение для признака xi;
R2 yx1x2…xp- множественный коэффициент детерминации всего комплекса р факторов с результатом;
R2 xix1x2… xp - тот же показатель детерминации для зависимости фактора xi со всеми другими факторами уравнения множественной регрессии;
n -k-1 –число степеней свободы для остаточной суммы квадратов отклонений.
Величина F – критерия, оценивая значимость уравнения регрессии в целом, характеризует одновременной и значимость коэффициента (индекса) множественной корреляции.
Аналогично можно оценивать и существенность частных показателей корреляции. Если величина частного критерия Фишера Fxi выше табличного, то это означает и значимость частного коэффициента корреляции.

