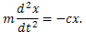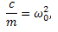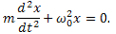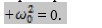приложенных к точке.
Свободные колебания (собственные), происходящие в представленной самой себе системе около положения равновесия после какого-либо первоначального воздействия.
Рассмотрим точку М, движущуюся прямолинейно под действием одной только восстанавливающей силы , направленной к неподвижному центру О и пропорциональной расстоянию от этого центра. Проекция силы на ось Ох (рис.1) будет равна Fx=-cx. Сила, как видим, стремится вернуть точку в равновесное положение О, где F=0; отсюда и наименование «восстанавливающая» сила. Примером такой силы является сила упругости. Коэффициент c пропорциональности называется жесткостью упругого элемента.
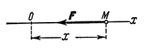
Любая другая сила, неупругая по природе, но удовлетворяющая соотношению F = – cx, называется квазиупругой.
Найдем закон движения точки М. Составляя дифференциальное уравнение движения получим
Деля обе части равенства на т и вводя обозначение
приведем уравнение к виду
Уравнение представляет собою дифференциальное уравнение свободных колебаний при отсутствии сопротивления. Решение этого линейного однородного дифференциального уравнения второго порядка ищут в виде x=ent. Полагая x=ent, получим для определения п так называемое характеристическое уравнение, имеющее в данном случае вид n2+
