Атомная орбиталь — одноэлектронная волновая функция в сферически симметричном электрическом поле атомного ядра, задающаяся главным n,орбитальным l и магнитным m квантовыми числами.
Название «орбиталь» (а не орбита) отражает геометрическое представление о стационарных состояниях электрона в атоме; такое особое название отражает тот факт, что состояния электрона в атоме описывается законами квантовой механики и отличается от классического движения по траектории. Совокупность атомных орбиталей с одинаковым значением главного квантового числа n составляют одну электронную оболочку.
Квантовые числа и номенклатура орбиталей
Радиальное распределение плотности вероятности для атомных орбиталей при различных n и l.
-
Главное квантовое число n может принимать любые целые положительные значения, начиная с единицы (n = 1,2,3, … ∞) и определяет общую энергию электрона на данной орбитали (энергетический уровень) :

Энергия для n = ∞ соответствует энергии одноэлектронной ионизации для данного энергетического уровня.
-
Орбитальное квантовое число (называемое также азимутальным или дополнительным квантовым числом) определяет момент импульса электрона и может принимать целые значения от 0 до n — 1 (l = 0,1, …, n — 1). Момент импульса при этом задаётся соотношением
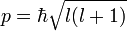
Атомные орбитали принято называть по буквенному обозначению их орбитального числа:
|
Значение орбитального квантового числа |
0 |
1 |
2 |
3 |
4 |
|
Буквенное обозначение |
s |
p |
d |
f |
g |
Магнитное квантовое число ml определяет проекцию орбитального момента импульса на направление магнитного поля и может принимать целые значения в диапазоне от -l до l, включая 0 (ml = -l … 0 … l):
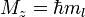
Волнова́я фу́нкция, или пси-функция 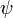 — комплекснозначная функция, используемая в квантовой механике для описания чистого состояния системы. Является коэффициентом разложения вектора состояния по базису (обычно координатному):
— комплекснозначная функция, используемая в квантовой механике для описания чистого состояния системы. Является коэффициентом разложения вектора состояния по базису (обычно координатному):
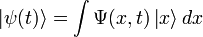
где 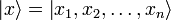 — координатный базисный вектор, а
— координатный базисный вектор, а 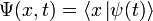 — волновая функция в координатном представлении. |ψ|2 – вероятность нахождения частицы в данной области пространства
— волновая функция в координатном представлении. |ψ|2 – вероятность нахождения частицы в данной области пространства
Пусть волновая функция задана в N-мерном пространстве, тогда в каждой точке с координатами 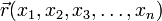 , в определенный момент времени t она будет иметь вид
, в определенный момент времени t она будет иметь вид 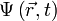 . В таком случае уравнение Шрёдингера запишется в виде:
. В таком случае уравнение Шрёдингера запишется в виде:
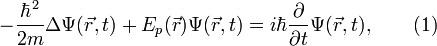
где 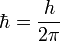 ,
, 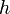 — постоянная Планка;
— постоянная Планка; 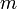 — масса частицы,
— масса частицы, 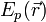 — внешняя по отношению к частице потенциальная энергия в точке
— внешняя по отношению к частице потенциальная энергия в точке 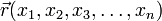 ,
,  — оператор Лапласа (или лапласиан), эквивалентен квадрату оператора набла
— оператор Лапласа (или лапласиан), эквивалентен квадрату оператора набла
Если атом связан с другими атомами ОДИНАКОВЫМИ СВЯЗЯМИ, но при их образовании участвуют орбитали разного типа, то используется метод ГИБРИДИЗАЦИИ.
Пример: Молекула СН4 имеет форму правильного тетраэдра, в ней все 4 связи имеют одинаковую длину, прочность, находятся под одинаковыми углами друг к другу.
Однако у четырёхвалентного атома углерода электроны расположены на трёх р-орбиталях и одной s-орбитали. Они разные по энергии, форме и расположены в пространстве иначе.
Для объяснения используется понятие ГИБРИДИЗАЦИИ:
из четырёх атомных орбиталей образуются 4 новых,
гибридных орбитали, которые в пространстве располагаются НА МАКСИМАЛЬНОМ УДАЛЕНИИ ДРУГ ОТ ДРУГА. Это правильный тетраэдр, углы между связями равны 109° 29´.

Так как в образовании четырёх связей участвуют одна s и три р-оболочки, то такой тип гибридизации обозначается sp3
В зависимости от числа и типа орбиталей, которые принимают участие в гибридизации, отличают следующие типы гибридизации:
1) sp-гибридизация. Участвуют одна s-орбиталь и одна р-орбиталь. Молекула имеет линейную структуру, валентный угол – 1800.

2) sp2-гибридизация. Участвуют одна s-орбиталь и две р-орбитали. Молекула располагается в плоскости (концы гибридных орбиталей направлены к вершинам равностороннего треугольника), валентный угол – 1200.

3) sp3-гибридизация. Участвуют одна s-орбиталь и три р-орбитали. Молекула имеет тетраэдрическую форму, валентный угол – 109,280.

4) sp3d-гибридизация. Форма молекулы - тригональная БИПИРАМИДА.

5) sp3d2-гибридизация, пример – SF6. Форма молекулы - ОКТАЭДР.


