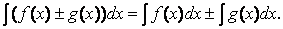Пусть f определена на (a,b) ->R. Функция F :(a,b)->R называется первообразной для f , если:
1) F дифференцируема на (a,b)
2) производная F(x) = f(x) на (a,b).
Пусть f:(a,b)->R, символом «∫f(x)dx» обозначается любая из первообразных функции f и называется неопределенный интеграл от f на (a,b)
1. Производная неопределенного интеграла равна подынтегральной функции, т.е.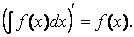
Действительно,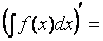 
(F(x)+C)' = F'(x) = f(x).
2. Дифференциал от неопределенного интеграла равен подынтегральному выражению, т.е.
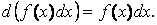
Действительно,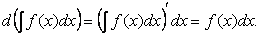 
3. Интеграл от дифференциала функции равен (с точностью до произвольной постоянной) самой функции, т.е.
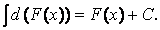
Действительно,
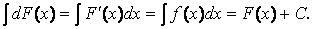
4. Постоянный множитель можно выносить за знак интеграла, т.е.
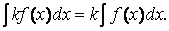
Действительно, если F(x) — первообразная для функции f(x), т.е. F'(x) = f(x), то kF(x) —первообразная для функции kf(x). Из определения 2 следует, что
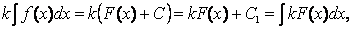где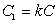 
.
5. Неопределенный интеграл от алгебраической суммы двух интегрируемых функций равен алгебраической сумме интегралов от слагаемых функций, т.е.
