Количеством движения системы будем называть векторную величину 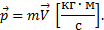, равную геомет­рической сумме (главному вектору) количеств движения всех точек системы (рис.44):

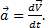
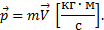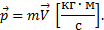Из чертежа видно, что независимо от величин скоростей точек системы (если только эти скорости не параллельны) вектор  может принимать любые значения и даже оказаться равным нулю, когда многоугольник, построенный из векторов , замкнется. Следова­тельно, по величине  нель­зя полностью судить о ха­рактере движения системы.                                                                

Рис.44

Найдем формулу, с по­мощью которой значительно легче вычислять величину 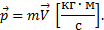, а также уяснить ее смысл.

Из равенства  следует, что 

Беря от обеих частей производную по времени, получим

 или  

Отсюда находим, что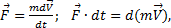 

т.е. количество движения системы равно произведению массы всей системы на скорость ее центра масс. Этим результатом особенно удобно пользоваться при вычислении количеств движения твердых тел.

Из формулы видно, что если тело (или система) движется так, что центр масс остается неподвижным, то количество движения тела равно нулю. Например, количество движения тела, вращающегося вокруг неподвижной оси, проходящей через его центр масс, будет равно нулю.

Если же движение тела является сложным, то величина 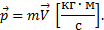 не будет характеризовать вращательную часть движения вокруг центра масс. Например, для катящегося колеса  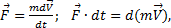независимо от того, как вращается колесо вокруг его центра масс С.

Таким образом, количество движения характеризует только поступательное движение системы. При сложном же движении величина 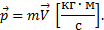 характеризует только поступательную часть движения системы вместе с центром масс.

Из теоремы об изменении количества движения системы можно получить следую­щие важные следствия:

1) Пусть сумма всех внешних сил, действующих на систему, равна нулю:

Тогда из уравнения 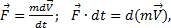 следует, что при этом 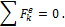. Таким образом, если сумма всех внешних сил, действующих на систему, равна нулю, то вектор количества движения системы будет постоянен по модулю и направлению.

2) Пусть внешние силы, действующие на систему, таковы, что сумма их проекций на какую-нибудь ось (например Оx) равна нулю:

Тогда из уравнения 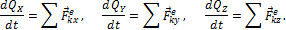 следует, что при этом 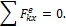. Таким образом, если сумма проекций всех действующих внешних сил на какую-нибудь ось равна нулю, то проекция количества движения системы на эту ось есть величина постоянная.

Эти результаты и выражают закон сохранения количества движения системы. Из них следует, что внутренние силы изменить суммарное количество движения системы не могут. Рассмотрим неко­торые примеры:

а) Явление отдачи или отката. Если рассматривать винтовку и пулю как одну систему, то давление пороховых газов при выстреле будет силой внутренней. Эта сила не может изменить суммарное количество движения системы. Но так как пороховые газы, действуя на пулю, сообщают ей некоторое количество движения, направленное вперед, то они одновременно должны сообщить винтовке такое же количество движения в обратном направлении. Это вызовет движение винтовки назад, т.е. так называемую отдачу. Аналогичное явление получается при стрельбе из орудия (откат).

б) Работа   гребного   винта   (пропеллера). Винт сообщает некоторой массе воздуха (или воды) движение вдоль оси винта, отбрасывая эту массу назад. Если рассматривать отбрасываемую массу и самолет (или судно) как одну систему, то силы взаимодействия винта и среды как внутренние не могут изменить суммарное коли­чество движения этой системы. Поэтому при отбрасывании массы воздуха (воды) назад самолет (или судно) получает соответствующую скорость движения вперед, такую, что общее количество движения рассматриваемой системы останется равным нулю, так как оно было нулем до начала движения.

Аналогичный эффект достигается действием весел или гребных колес.

в) Реактивное движение. В реактивном снаряде (ракете) газообразные продукты горения топлива с большой скоростью выбрасываются из отверстия в хвостовой части ракеты (из сопла реактивного двигателя). Действующие при этом силы давления бу­дут силами внутренними, и они не могут изменить суммарное коли­чество движения системы ракета - продукты горения топлива. Но так как вырывающиеся газы имеют известное количество движения, на­правленное назад, то ракета получает при этом соответствующую скорость движения вперед.