Рассмотрим систему, состоящую из п материальных точек. Составим для этой системы дифференциальные уравнения движения и сложим их почленно. Тогда получим:
.
Последняя сумма по свойству внутренних сил равна нулю. Кроме того,
Окончательно находим:
.
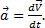Уравнение выражает теорему об изменении количества движения системы в дифференциальной форме: производная по времени от количества движения системы равна геометрической сумме всех действующих на систему внешних сил. В проекциях на координатные оси будем иметь:
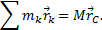
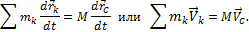
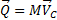
Найдем другое выражение теоремы. Пусть в момент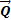 
количество движения системы равно 
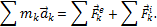, а в момент 
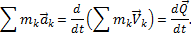становится равным 
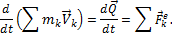. Тогда, умножая обе части равенства 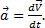на dt и интегрируя, получим:
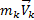
или
так как интегралы, стоящие справа, дают импульсы внешних сил.
Уравнение выражает теорему об изменении количества движения системы в интегральной форме: изменение количества движения системы за некоторый промежуток времени равно сумме импульсов действующих на систему внешних сил за тот же промежуток времени.
В проекциях на координатные оси будем иметь:
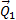
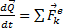
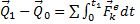
Укажем на связь между доказанной теоремой и теоремой о движении центра масс. Так как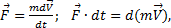 
то, подставляя это значение в равенство и учитывая, что 
, мы получим 
.
Следовательно, теорема о движении центра масс и теорема об изменении количества движения системы представляют собой, по существу, две разные формы одной и той же теоремы. В тех случаях, когда изучается движение твердого тела (или системы тел), можно в равной мере пользоваться любой из этих форм.
Практическая ценность теоремы состоит в том, что она позволяет исключить из рассмотрения наперед неизвестные внутренние силы (например, силы давления друг на друга частиц жидкости).
