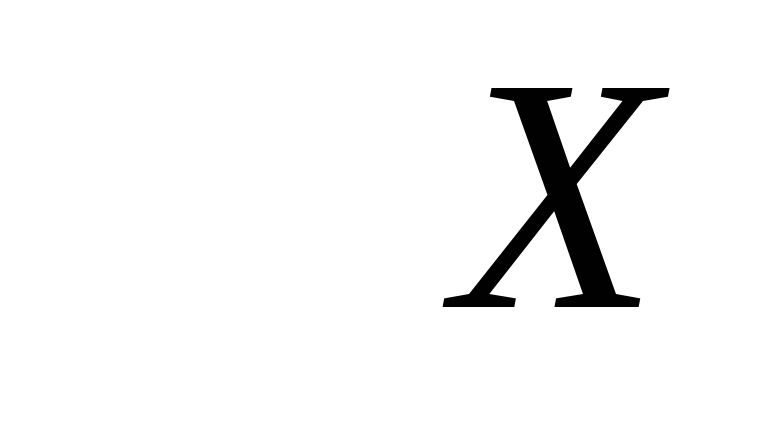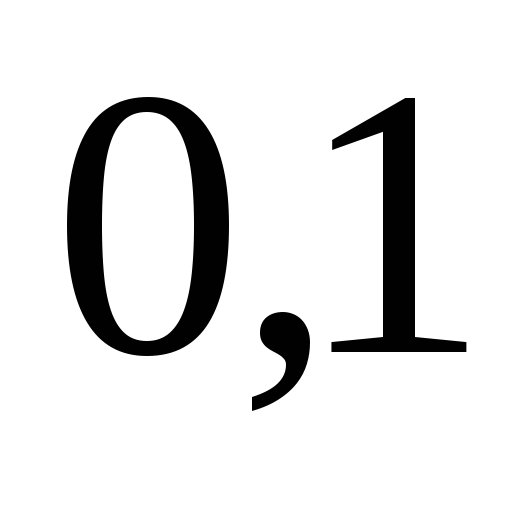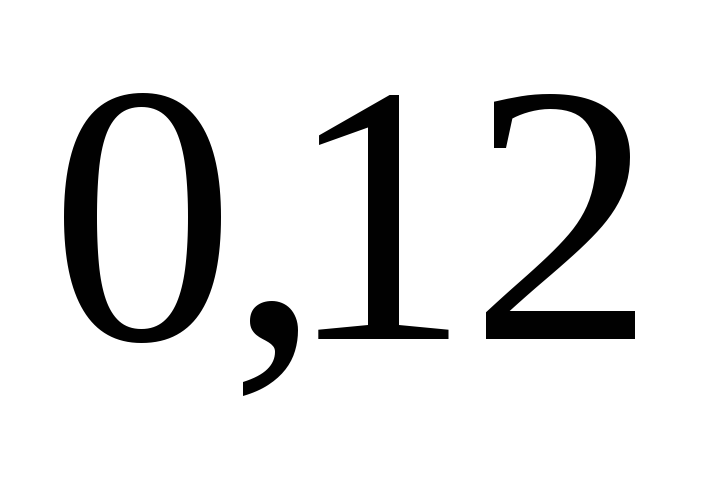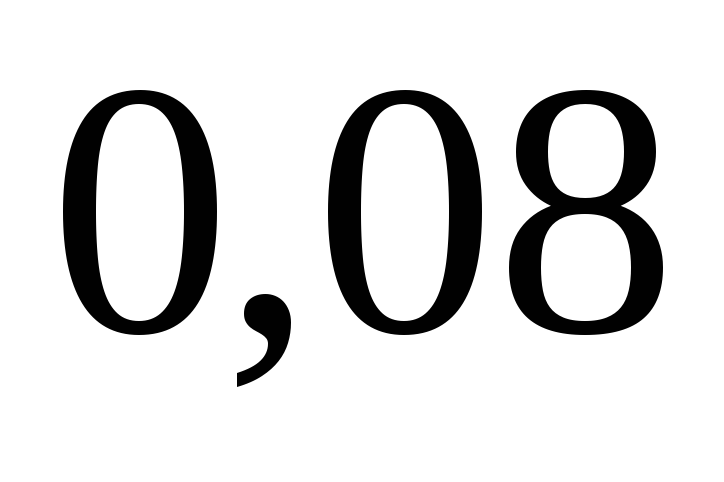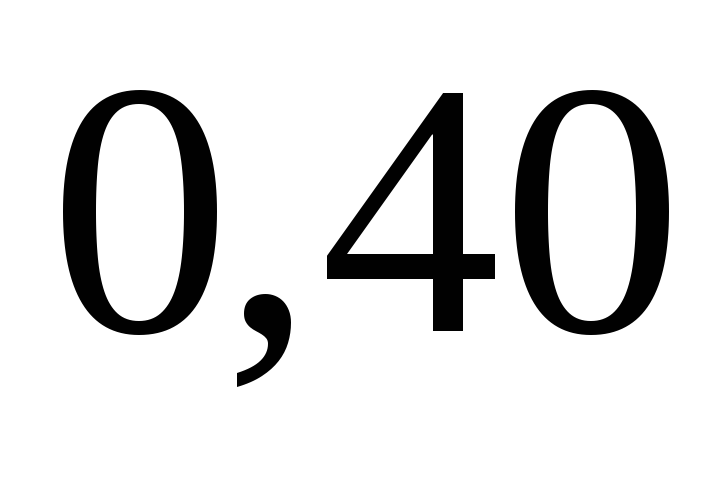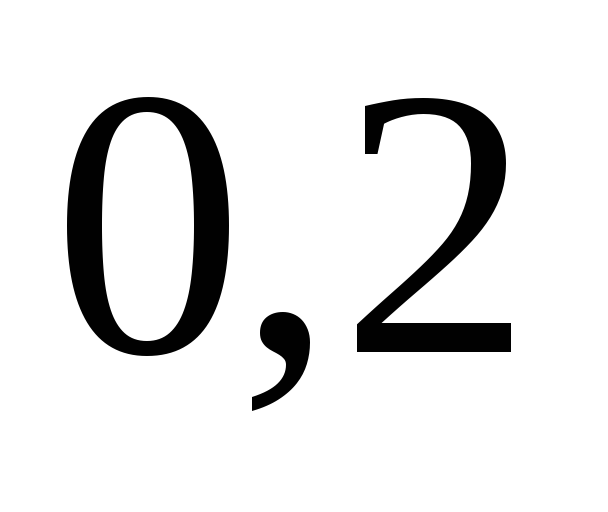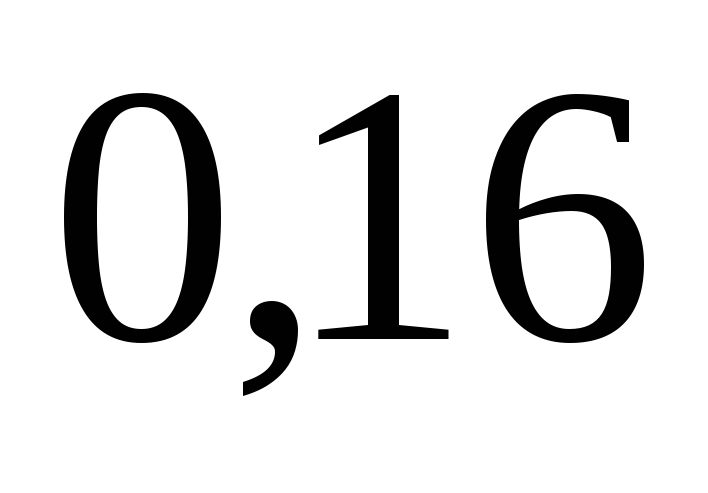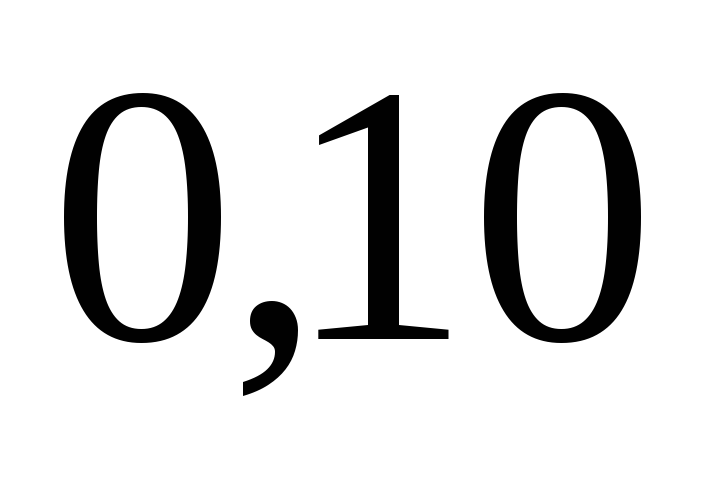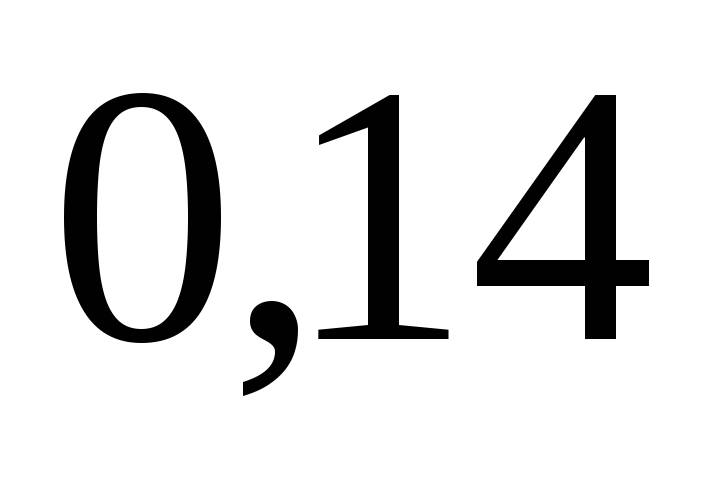Условные законы распределения составляющихсистемы дискретных случайных величин

Если случайные величины 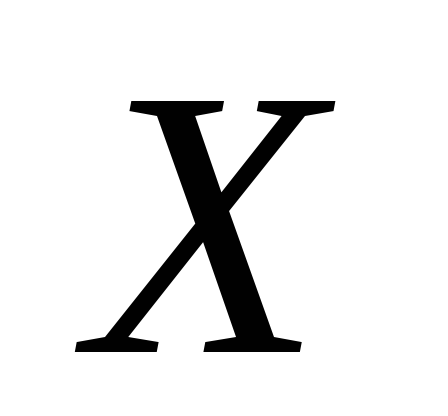иобразуют зависимую систему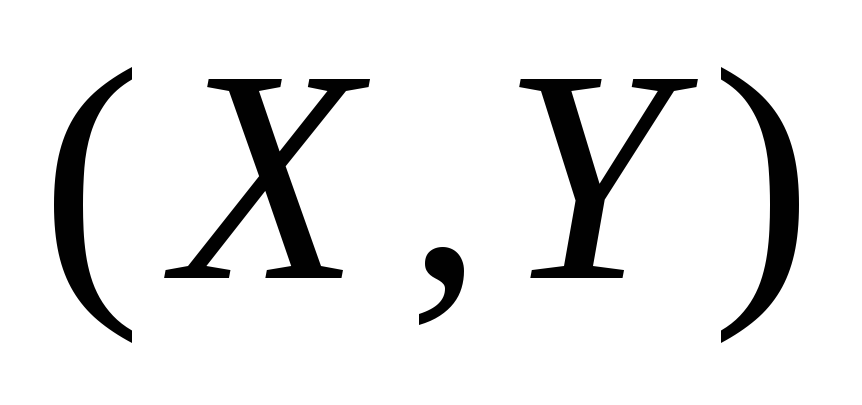между собой, то дляхарактеристики уровня их зависимости вводится понятие условных законов распределения случайных величин.

Ранее было установлено, что если события A и B зависимы, то условная вероятность события B отличается от его безусловной вероятности. В этом случае напомним, что имели место равенства:

(23) 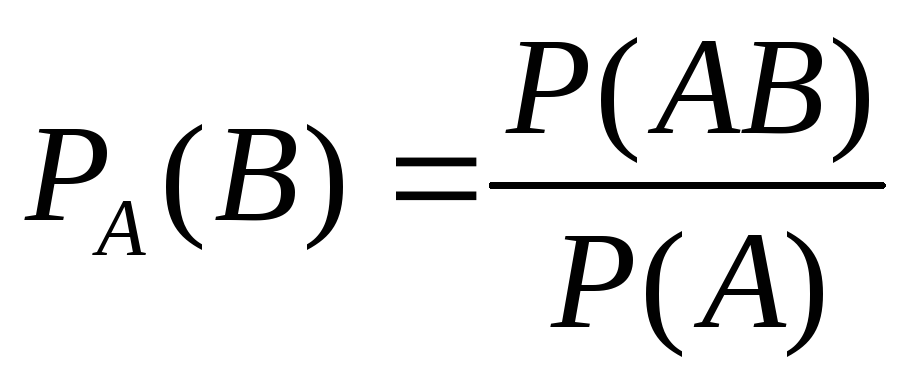или.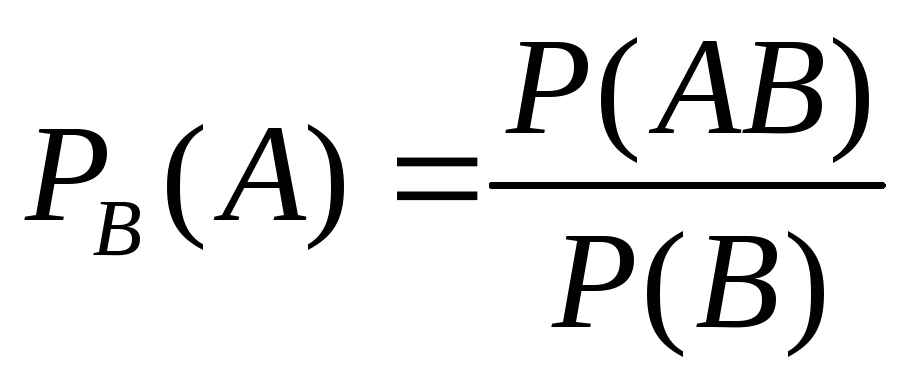

Аналогичное положение имеет место и для двумерных случайных величин.

Рассмотрим дискретную двумерную случайную величину (X, Y). Пусть возможные значения составляющих таковы

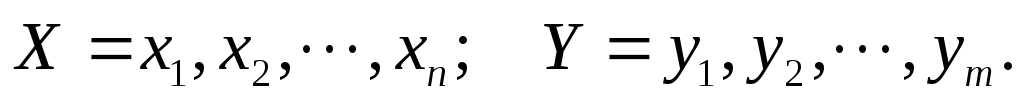
Допустим, что в результате испытания другая величина Y приняла определённое значение 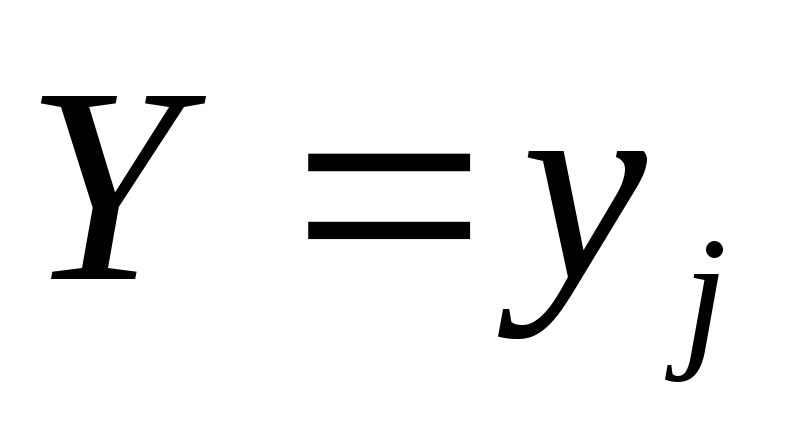(или попала в определённый интервал числовой оси); при этомX примет одно из своих возможных значений 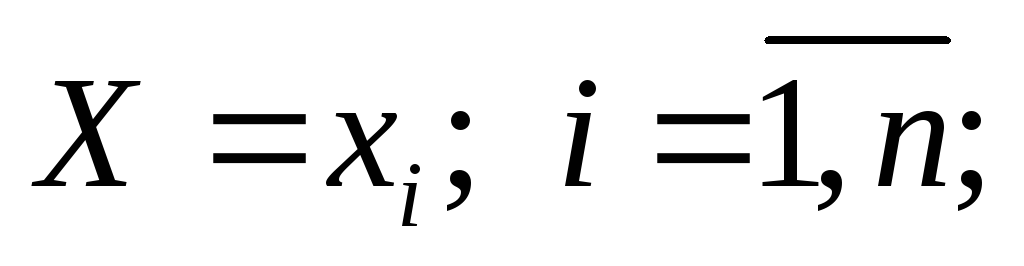. Обозначим условную вероятность того, что X примет, например значение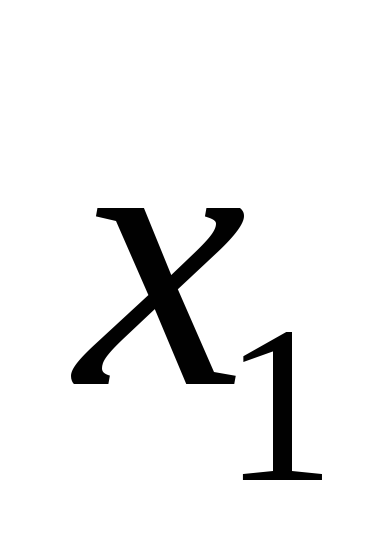при условии, что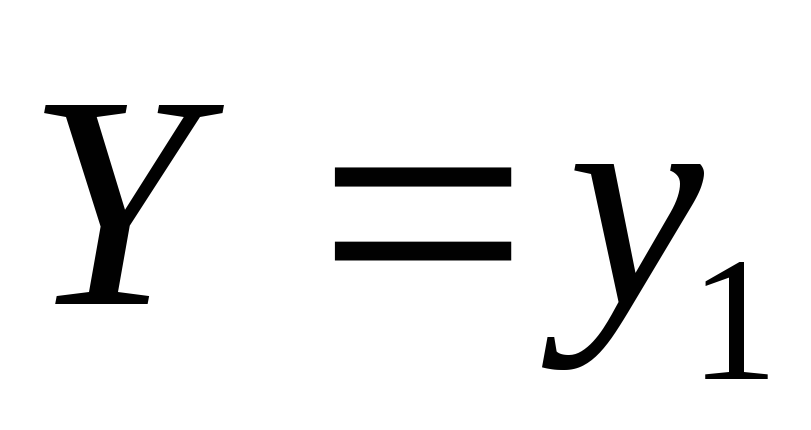, через 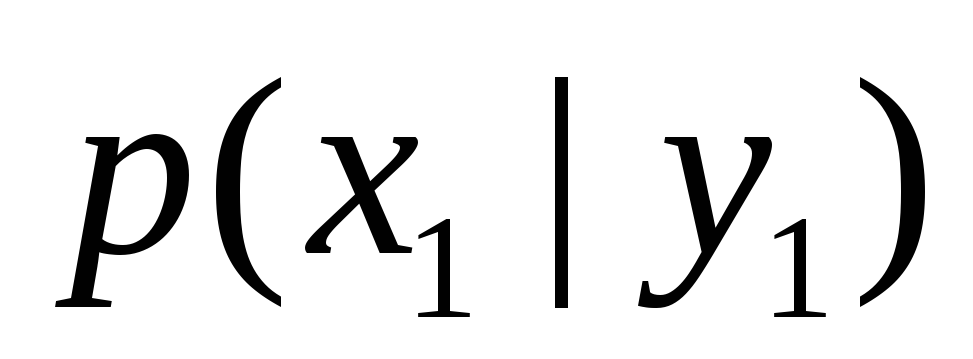. Эта вероятность, вообще говоря, не будет равна безусловной вероятности .

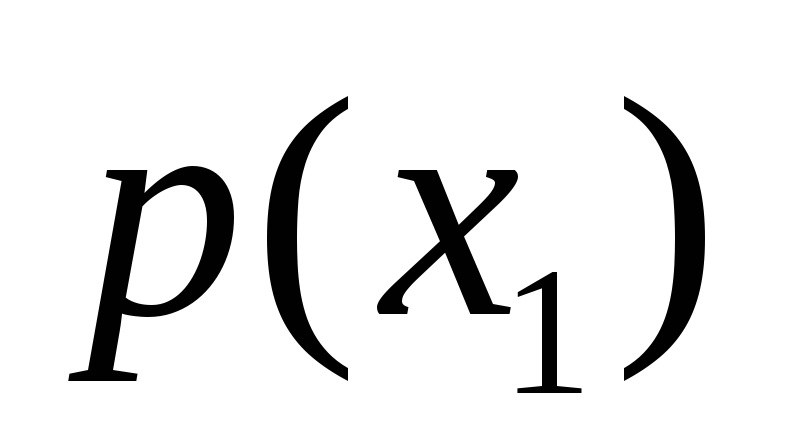Условная вероятностью, что с.в. 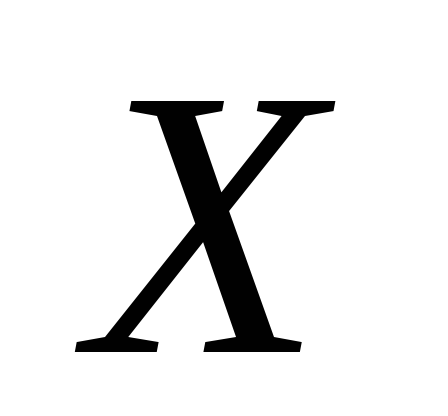примет значение 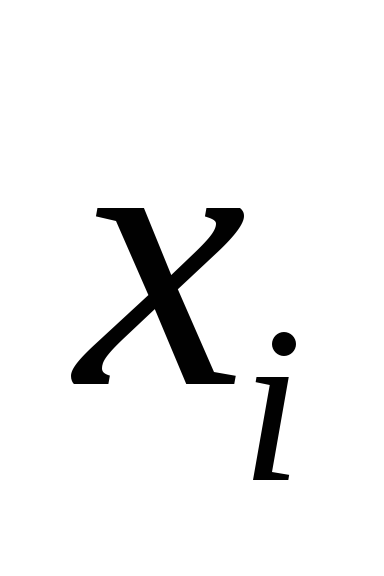при условии  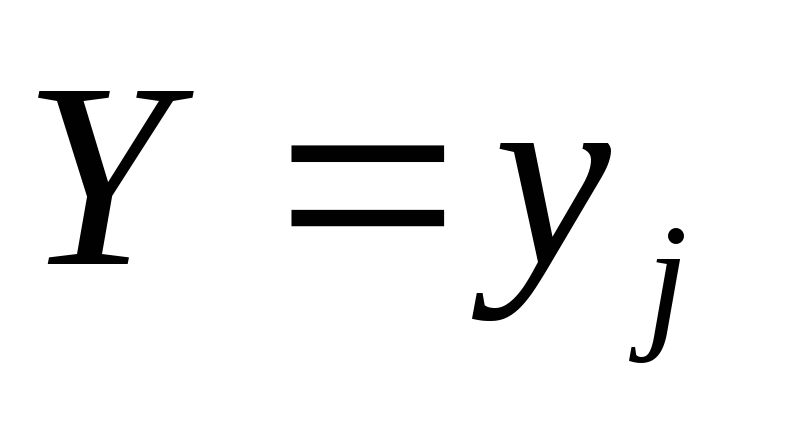(имеет одно и то же значение при всех значенияхX) определяется равенством

(24) 

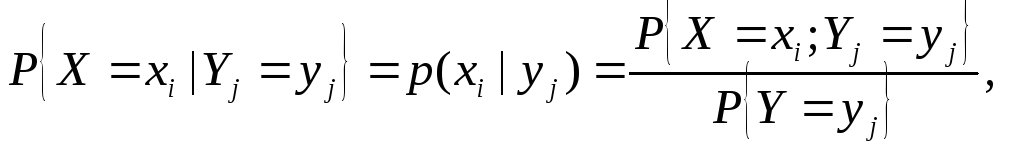
где (i=1, 2, ..., n; j=1, 2, ..., m), (или коротко: ),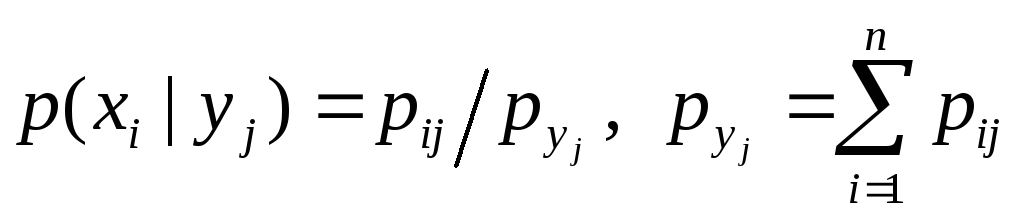

найденных в предположении, что событие 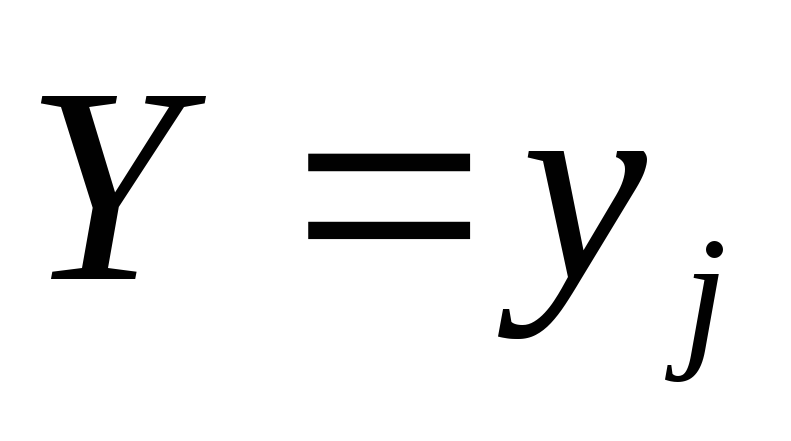уже наступило. Совокупность вероятностей (20), т.е. совокупностью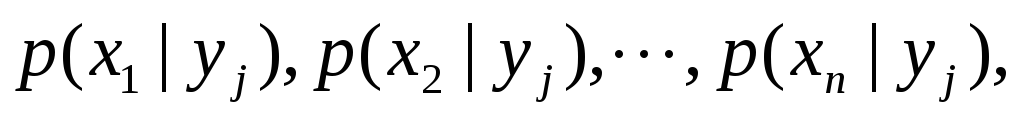представляет собой «условный закон распределения случайной величины 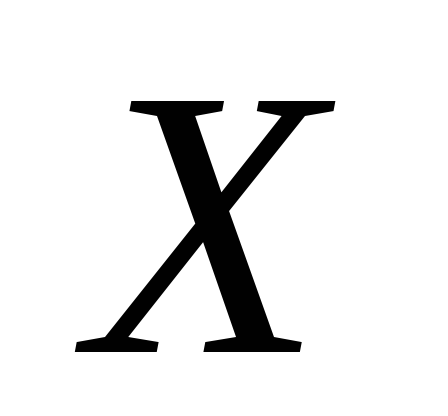при условии 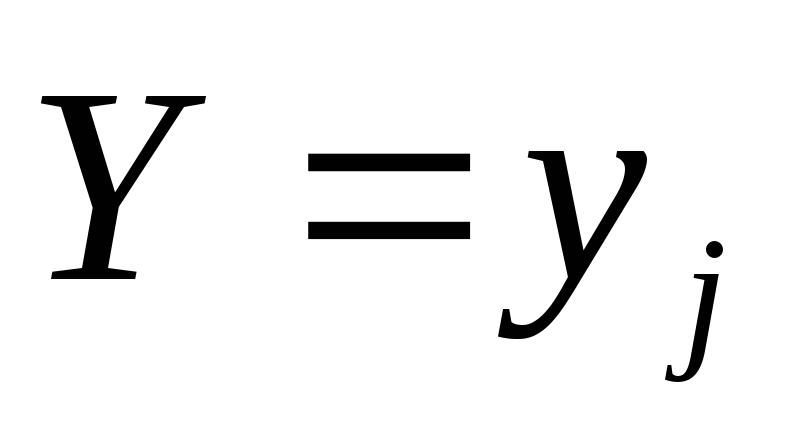». Сумма условных вероятностей равна 1, действительно

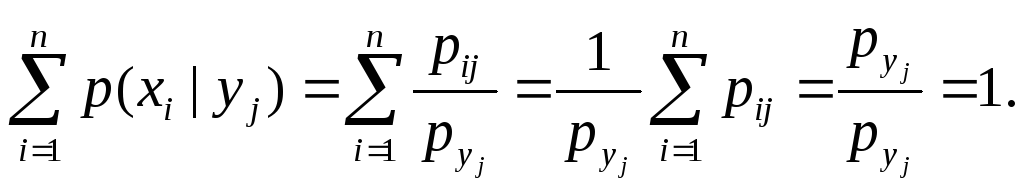
Аналогично определяется условная вероятность, условный закон распределения случайной величины при условии, что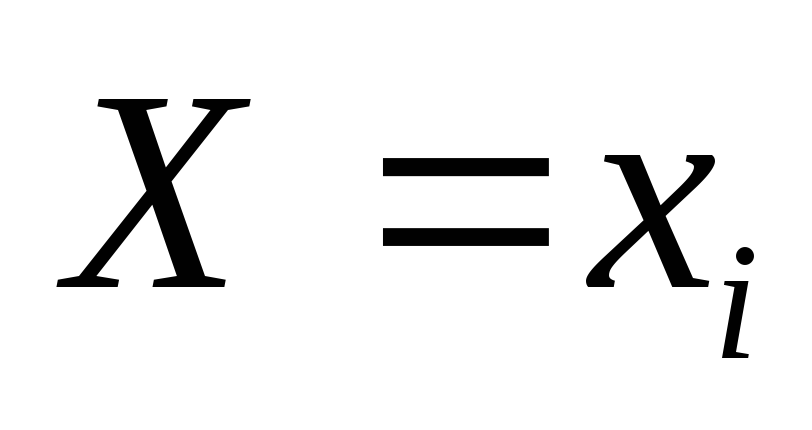(событие уже наступило)

(25) 

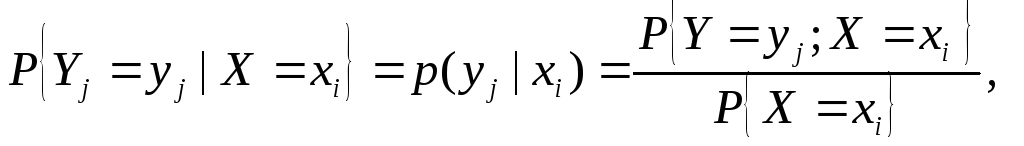
где (i=1, 2, ..., n; j=1, 2, ..., m), (или коротко: ).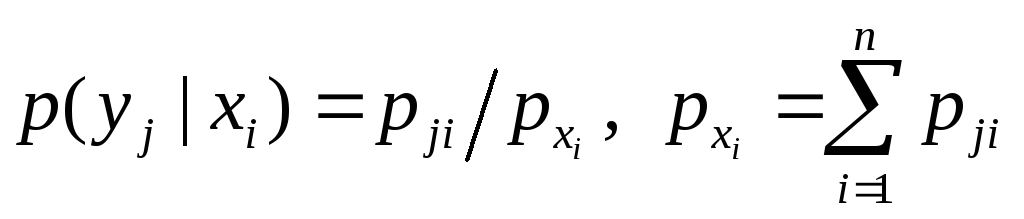

Также выполняется

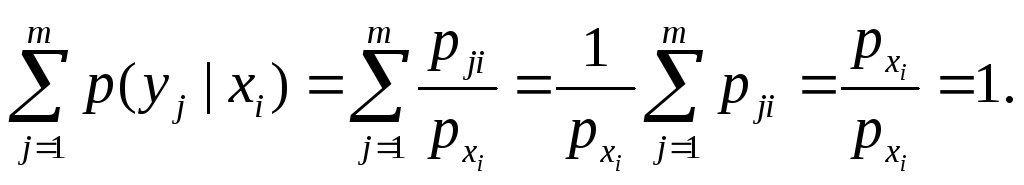
Зная закон распределения двумерной дискретной случайной величины, пользуясь формулой (23), можно вычислить условные законы распределения составляющих. Например, условный закон распределения 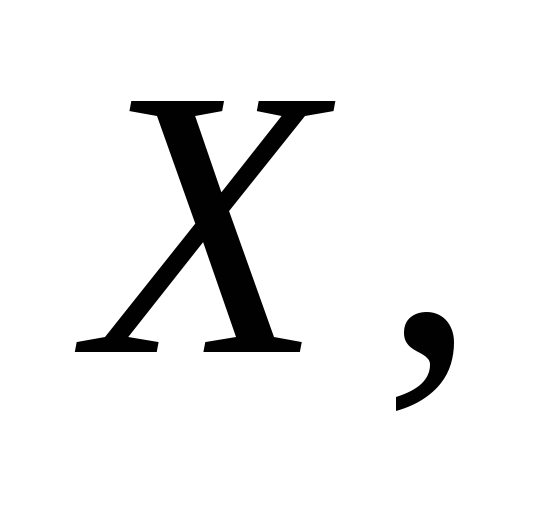в предположении, что событиеуже произошло, может быть найден по формуле

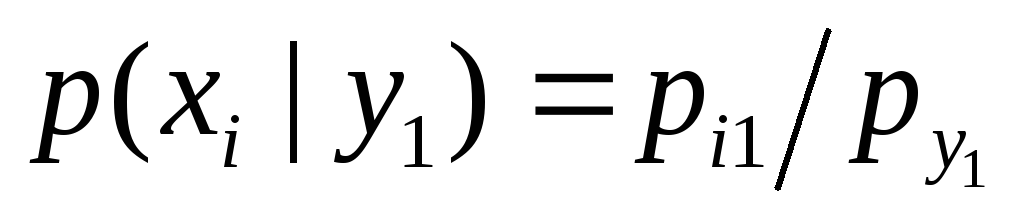
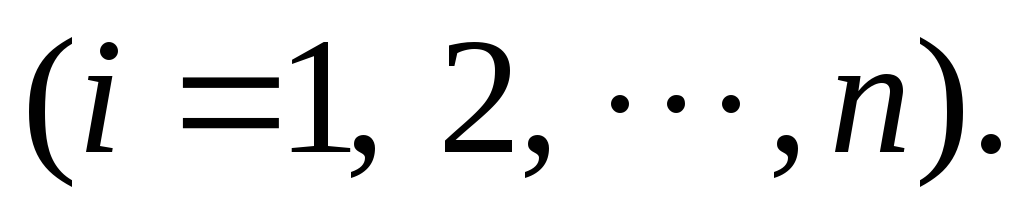
В общем случае условные законы распределения составляющей 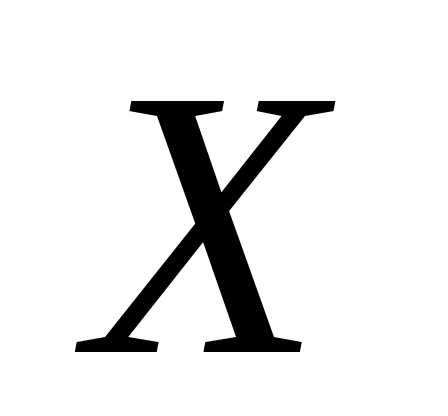определяются соотношением

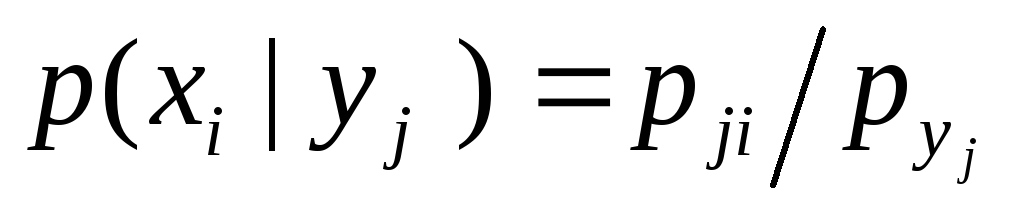
Аналогично находят условные законы распределения составляющей Y:

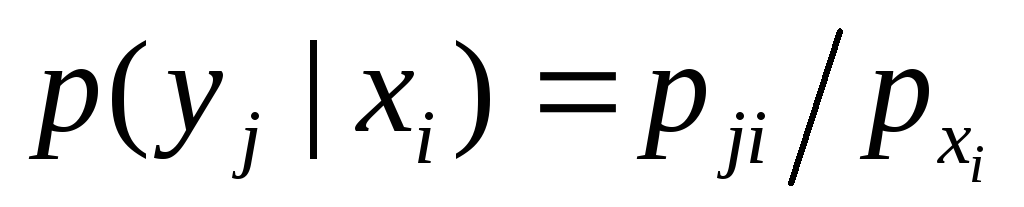
Пример 13. Двумерная случайная величина задана таблицей

Найти: а) безусловные законы распределения случайных величин X и ;

б) условный закон распределения случайной величины 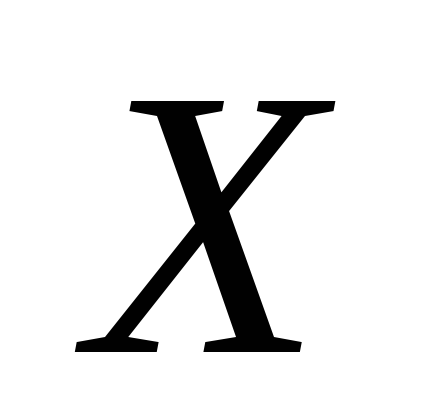 при .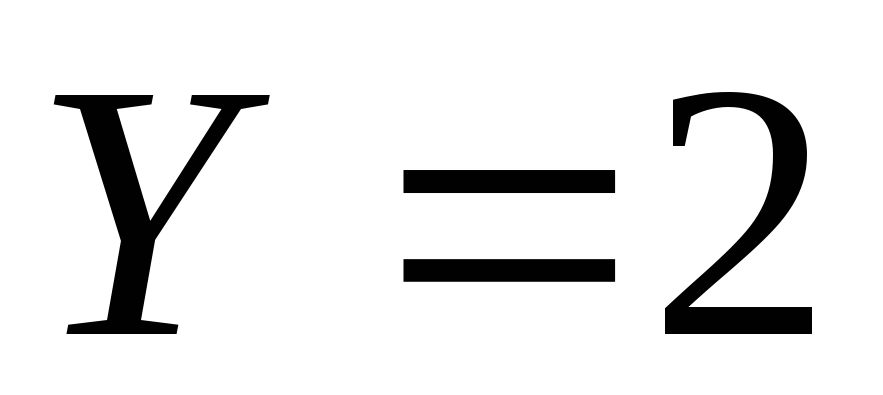

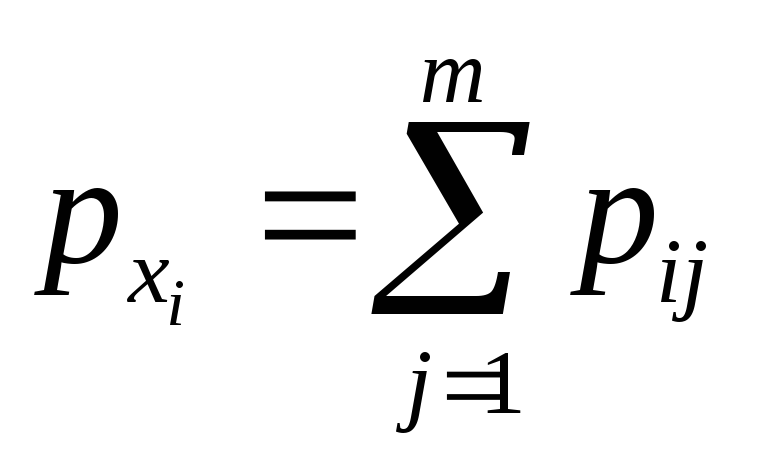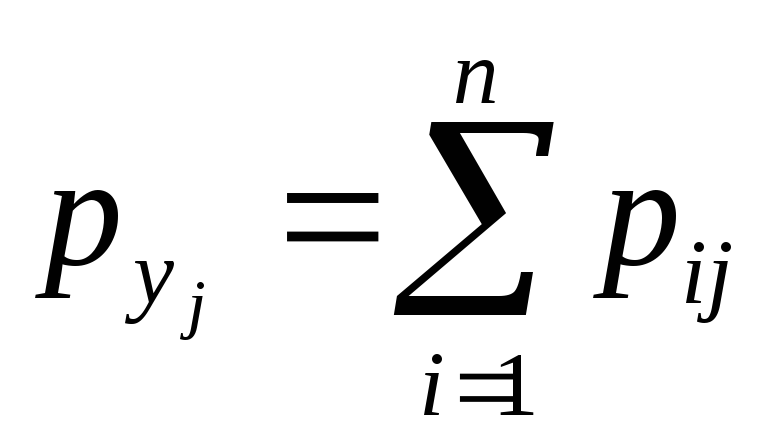Решение. а) Так как и, то

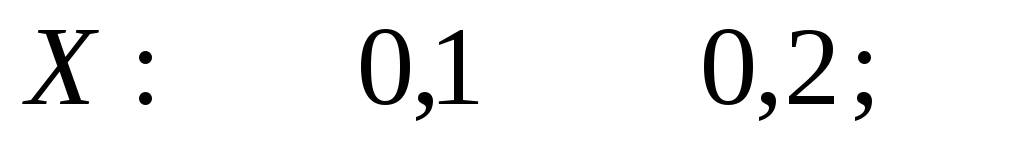
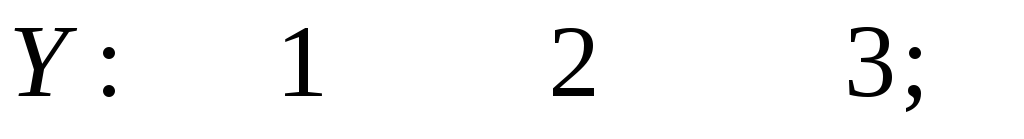
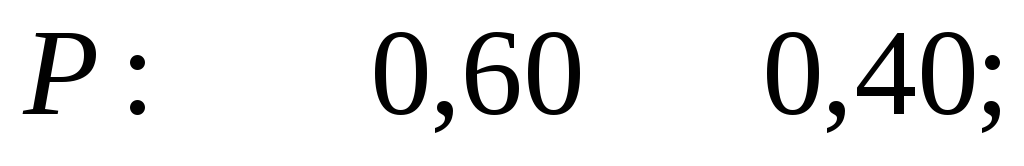
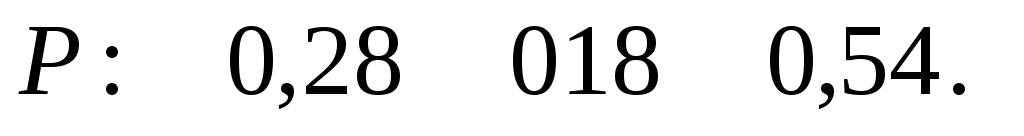
б) С учетом формулы (20) имеем

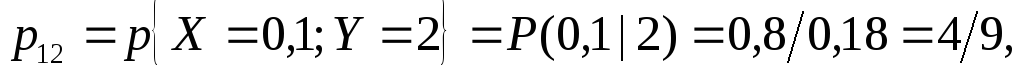
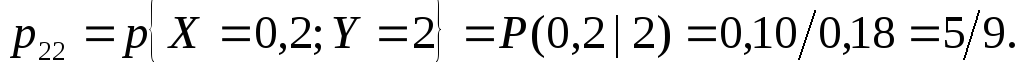
Таким образом, условный закон распределения случайной величины 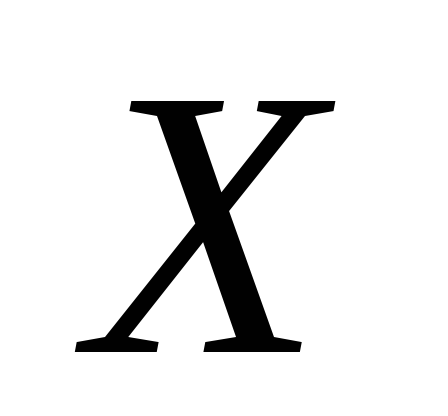при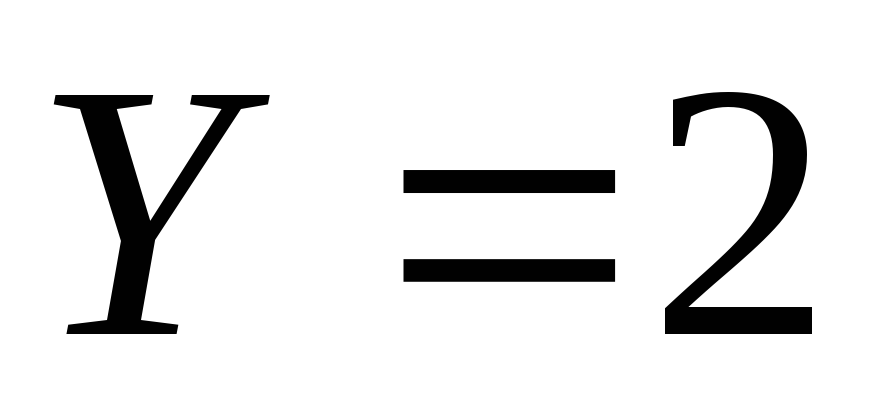таков:

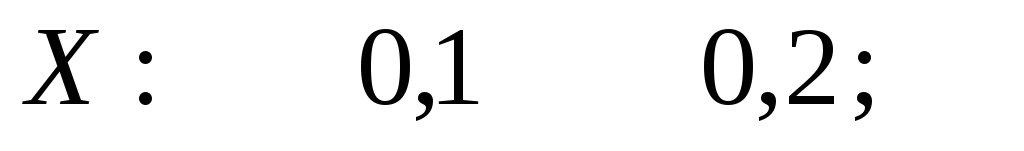
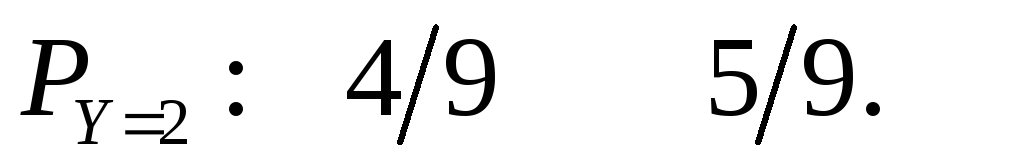
Контроль: 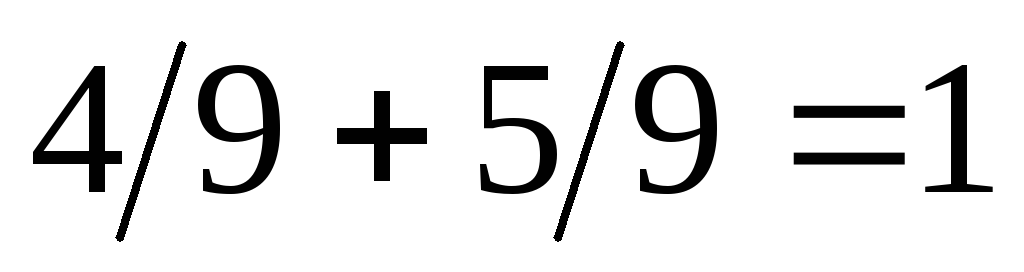. В этом примере очевидно несовпадение условного и безусловного законов распределения случайной величины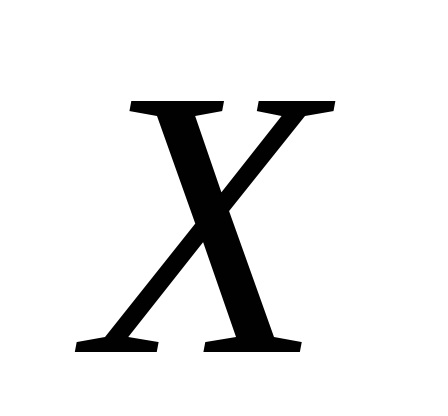. Следовательно, с.в.X и зависимы.

Задание. Найти условные законы вероятности с.в. пр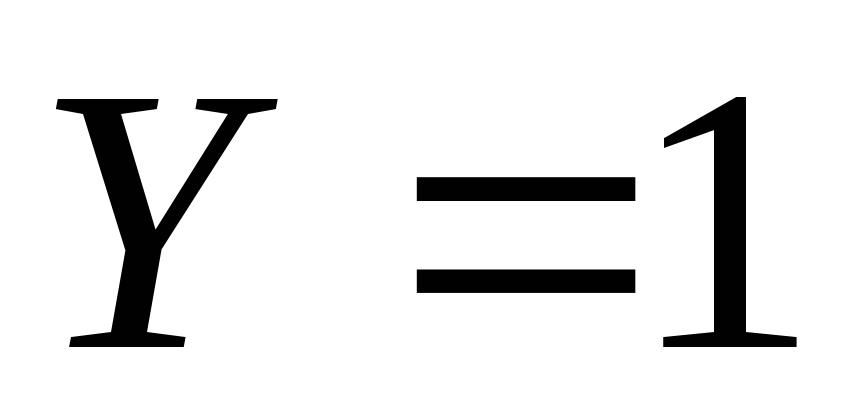и и.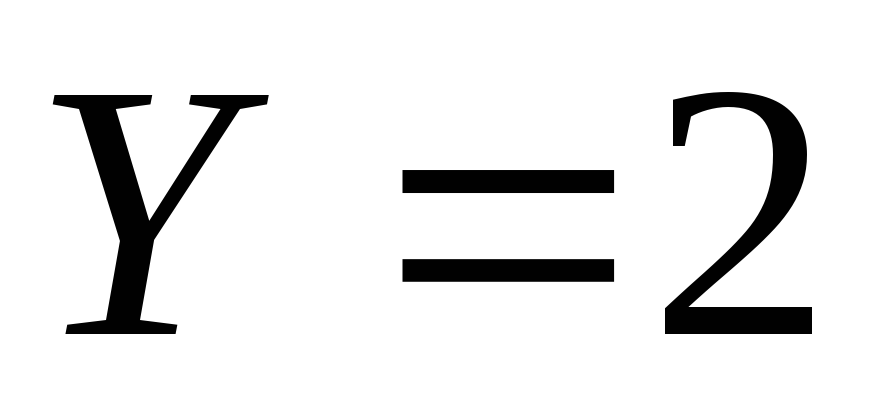

Записать эти законы распределения в каждом случае и проверить соответственно выполнения контроля.