В задачах 13.1 – 13.10 заданы математическое ожидание а и среднее квадратическое отклонение σ нормально распределённой случайной величины X. Требуется найти:
а) вероятность того, что X примет значение, принадлежащее интервалу (a , b );
б) вероятность того, что абсолютная величина отклонения X-а окажется меньше d.
Нормально распределенные непрерывные случайные величины встречаются в практических задачах чаще всего. Это связано, в частности, с Центральной предельной теоремой Ляпунова, которая утверждает, что если случайная величина порождена несколькими примерно равными по силе причинами, то она становится нормально (или почти нормально) распределенной.
Плотность (дифференциальная функция) нормального распределения равна 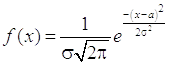 , т.е. зависит от двух параметров: математического ожидания a и среднего квадратического отклонения σ. Интегральная функция нормального распределения связана с функцией Лапласа
, т.е. зависит от двух параметров: математического ожидания a и среднего квадратического отклонения σ. Интегральная функция нормального распределения связана с функцией Лапласа 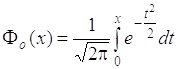 , значения которой берутся из таблиц (см.ниже). Для вычисления вероятности того, что нормально распределенная случайная величина X будет принимать значения в промежутке (α β) используется формула
, значения которой берутся из таблиц (см.ниже). Для вычисления вероятности того, что нормально распределенная случайная величина X будет принимать значения в промежутке (α β) используется формула 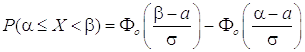 .
.
ПРИМЕР ЗАДАЧИ. Случайная величина X распределена нормально. Её математическое ожидание a = 2, а среднее квадратическое отклонение σ. Найти вероятность того, что в результате испытания Х примет значение, принадлежащее интервалу (1; 4).
Решение. Воспользуемся калькулятором 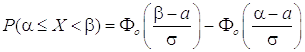 .
.
По условию a=2, σ=5, α=1, β=4, следовательно, 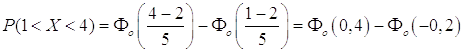
Так как функция Лапласа нечетна, то Фo(-0.2) = Фo(0.2)
Таким образом, P(1 < X < 4) = Фo(0.4) + Фo(0.2).
По таблице значений функции Лапласа (см. ниже) находим: Фo(0.4)=0.155; Фo(0.2)=0.079.
Таким образом, искомая вероятность равна P(1 < X < 4) = 0.234
Вычисление вероятности заданного отклонения. Правило трех сигм
Часто требуется вычислить вероятность того, что отклонение нормально распределенной случайной величины  по абсолютной величине меньше заданного положительного числа
по абсолютной величине меньше заданного положительного числа 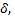 т.е. требуется найти вероятность осуществления неравенства
т.е. требуется найти вероятность осуществления неравенства
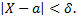
Перейдем к двойному неравенству
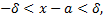
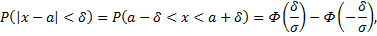
так как
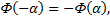
то
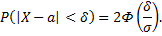
События, состоящие в осуществление неравенств

противоположные.
Поэтому, если вероятность осуществления неравенства
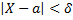
равна 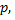 то вероятность неравенства
то вероятность неравенства
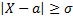
равна 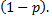
Рассмотрим пример. Случайная величина  распределена нормально. Математическое ожидание и среднее квадратическое отклонение
распределена нормально. Математическое ожидание и среднее квадратическое отклонение  соответственно равны 20 и 10. Найти вероятность того, что отклонение по абсолютной величине будет меньше трех.
соответственно равны 20 и 10. Найти вероятность того, что отклонение по абсолютной величине будет меньше трех.
По условию
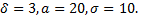
Тогда
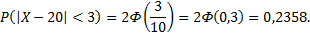
Правило трех сигм.
Преобразуем формулу
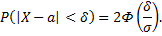
Пусть 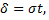 тогда
тогда
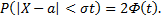
Если 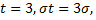 то
то
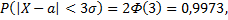
т.е. вероятность того, что отклонение по абсолютной величине будет меньше утроенного среднего квадратического отклонения, равна 0,9973. Другими словами, вероятность того, что абсолютная величина отклонения превысит утроенное среднее квадратическое отклонение, очень мала, а именно 0,0027.
В этом и состоит правило трех сигм: если случайная величина распределена нормально, то абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения.
На практике применяют правило трех сигм в случаях: если распределение изучаемой случайной величины неизвестно, но условие, указанное в приведенном правиле, выполняется, то есть основание предполагать, что изучаемая случайная величина распределена нормально; в противном случае, случайная величина не распределена нормально.

