Данная статья является естественным продолжением урока о независимых испытаниях, на котором мы познакомились с формулой Бернулли и отработали типовые примеры по теме. Локальная и интегральная теоремы Лапласа (Муавра-Лапласа) решают аналогичную задачу с тем отличием, что они применимы к достаточно большому количеству независимых испытаний. Не нужно тушеваться слов «локальная», «интегральная», «теоремы» – материал осваивается с той же лёгкостью, с какой Лаплас потрепал кучерявую голову Наполеона. Поэтому безо всяких комплексов и предварительных замечаний сразу же рассмотрим демонстрационный пример:
Монета подбрасывается 400 раз. Найти вероятность того, что орёл выпадет 200 раз.
По характерным признакам здесь следует применить формулу Бернулли 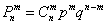 . Вспомним смысл этих букв:
. Вспомним смысл этих букв:
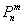 – вероятность того, что в
– вероятность того, что в 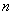 независимых испытаниях случайное событие
независимых испытаниях случайное событие 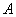 наступит ровно
наступит ровно 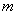 раз;
раз;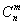 – биномиальный коэффициент;
– биномиальный коэффициент;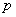 – вероятность появления события
– вероятность появления события 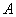 в каждом испытании;
в каждом испытании;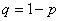 – вероятность противоположного события.
– вероятность противоположного события.
Применительно к нашей задаче: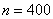 – общее количество испытаний;
– общее количество испытаний;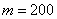 – количество бросков, в которых должен выпасть орёл;
– количество бросков, в которых должен выпасть орёл;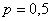 – вероятность выпадения орла в каждом броске;
– вероятность выпадения орла в каждом броске;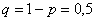 – вероятность выпадения решки.
– вероятность выпадения решки.
Таким образом, вероятность того, что в результате 400 бросков монеты орёл выпадет ровно 200 раз: 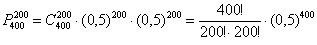 …Стоп, что делать дальше? Микрокалькулятор (по крайне мере, мой) не справился с 400-й степенью и капитулировал перед факториалами. А считать через произведение что-то не захотелось =) Воспользуемся стандартной функцией Экселя, которая сумела обработать монстра:
…Стоп, что делать дальше? Микрокалькулятор (по крайне мере, мой) не справился с 400-й степенью и капитулировал перед факториалами. А считать через произведение что-то не захотелось =) Воспользуемся стандартной функцией Экселя, которая сумела обработать монстра: 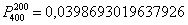 .
.
Заостряю ваше внимание, что получено точное значение и такое решение вроде бы идеально. На первый взгляд. Перечислим веские контраргументы:
– во-первых, программного обеспечения может не оказаться под рукой;
– и во-вторых, решение будет смотреться нестандартно (с немалой вероятностью придётся перерешивать);
Поэтому, уважаемые читатели, в ближайшем будущем нас ждёт:
Локальная теорема Лапласа
Если вероятность 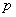 появления случайного события
появления случайного события 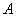 в каждом испытании постоянна, то вероятность
в каждом испытании постоянна, то вероятность 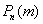 того, что в
того, что в 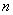 испытаниях событие
испытаниях событие 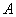 наступит ровно
наступит ровно 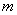 раз, приближённо равна:
раз, приближённо равна: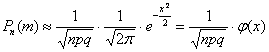 , где
, где 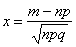 .
.
При этом, чем больше 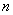 , тем рассчитанная вероятность
, тем рассчитанная вероятность 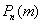 будет лучше приближать точное значению
будет лучше приближать точное значению 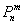 , полученное (хотя бы гипотетически) по формуле Бернулли. Рекомендуемое минимальное количество испытаний – примерно 50-100, в противном случае результат
, полученное (хотя бы гипотетически) по формуле Бернулли. Рекомендуемое минимальное количество испытаний – примерно 50-100, в противном случае результат 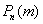 может оказаться далёким от истины. Кроме того, локальная теорема Лапласа работает тем лучше, чем вероятность
может оказаться далёким от истины. Кроме того, локальная теорема Лапласа работает тем лучше, чем вероятность 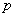 ближе к 0,5, и наоборот – даёт существенную погрешность при значениях
ближе к 0,5, и наоборот – даёт существенную погрешность при значениях 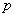 , близких к нулю либо единице. По этой причине ещё одним критерием эффективного использования формулы
, близких к нулю либо единице. По этой причине ещё одним критерием эффективного использования формулы 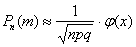 является выполнение неравенства
является выполнение неравенства 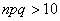 (
(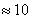 ).
).
Так, например, если 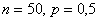 , то
, то 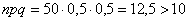 и применение теоремы Лапласа для 50 испытаний оправдано. Но если
и применение теоремы Лапласа для 50 испытаний оправдано. Но если 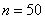 и
и 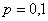 , то
, то 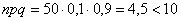 и приближение
и приближение 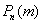 (к точному значению
(к точному значению 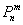 ) будет плохим.
) будет плохим.
О том, почему 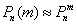 и об особенной функции
и об особенной функции 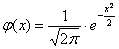 мы поговорим на уроке о нормальном распределении вероятностей, а пока нам потребуется формально-вычислительная сторона вопроса. В частности, важным фактом является чётность этой функции:
мы поговорим на уроке о нормальном распределении вероятностей, а пока нам потребуется формально-вычислительная сторона вопроса. В частности, важным фактом является чётность этой функции: 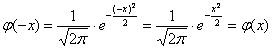 .
.
Оформим официальные отношения с нашим примером:
Задача 1
Монета подбрасывается 400 раз. Найти вероятность того, что орёл выпадет ровно:
а) 200 раз;
б) 225 раз.
С чего начать решение? Сначала распишем известные величины, чтобы они были перед глазами:
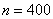 – общее количество независимых испытаний;
– общее количество независимых испытаний;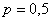 – вероятность выпадения орла в каждом броске;
– вероятность выпадения орла в каждом броске;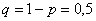 – вероятность выпадения решки.
– вероятность выпадения решки.
а) Найдём вероятность того, что в серии из 400 бросков орёл выпадет ровно 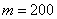 раз. Ввиду большого количества испытаний используем локальную теорему Лапласа:
раз. Ввиду большого количества испытаний используем локальную теорему Лапласа: 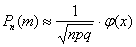 , где
, где 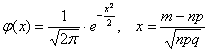 .
.
На первом шаге вычислим требуемое значение аргумента: 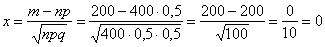
Далее находим соответствующее значение функции: 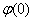 . Это можно сделать несколькими способами. В первую очередь, конечно же, напрашиваются непосредственные вычисления:
. Это можно сделать несколькими способами. В первую очередь, конечно же, напрашиваются непосредственные вычисления: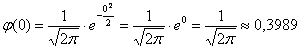
Округление проводят, как правило, до 4 знаков после запятой.
Недостаток прямого вычисления состоит в том, что экспоненту переваривает далеко не каждый микрокалькулятор, кроме того, расчёты не особо приятны и отнимают время. Зачем так мучиться? Используйте калькулятор по терверу (пункт 4) и получайте значения 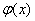 моментально!
моментально!
Кроме того, существует таблица значений функции 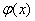 , которая есть практически в любой книге по теории вероятностей, в частности, в учебном пособии В.Е. Гмурмана. Закачайте, кто ещё не закачал – там вообще много полезного ;-) И обязательно научитесь пользовать таблицей (прямо сейчас!) – подходящей вычислительной техники всегда может не оказаться под рукой!
, которая есть практически в любой книге по теории вероятностей, в частности, в учебном пособии В.Е. Гмурмана. Закачайте, кто ещё не закачал – там вообще много полезного ;-) И обязательно научитесь пользовать таблицей (прямо сейчас!) – подходящей вычислительной техники всегда может не оказаться под рукой!
На заключительном этапе применим формулу 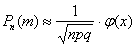 :
: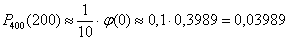 – вероятность того, что при 400 бросках монеты орёл выпадет ровно 200 раз.
– вероятность того, что при 400 бросках монеты орёл выпадет ровно 200 раз.
Как видите, полученный результат очень близок к точному значению 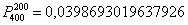 , вычисленному по формуле Бернулли.
, вычисленному по формуле Бернулли.
б) Найдём вероятность того, что в серии из 400 испытаний орёл выпадет ровно 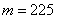 раз. Используем локальную теорему Лапласа. Раз, два, три – и готово:
раз. Используем локальную теорему Лапласа. Раз, два, три – и готово:
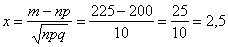
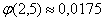
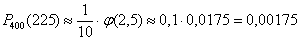 – искомая вероятность.
– искомая вероятность.
Ответ: 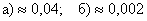
Формула Бернулли:

где P(k) - вероятность появления события A ровно k раз при n независимых испытаний, p - вероятность появления события A при каждом испытании.


