|
Вероятность того, что произойдет, по крайней мере, одно из событий определяется по формуле:
Теорема 5. Вероятность появления хотя бы одного из событий (А1, А2,…,Аn), независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий.
Пример 10. Студент сдает два экзамена в сессию. Вероятность сдать первый экзамен р1=0,8. Вероятность сдать второй экзамен р2=0,7. Какова вероятность, что студент сдаст хотя бы один экзамен в сессию. Решение. Вероятность события «не сдать первый экзамен» равна: q1=1–р1=1–0,8 = 0,2. Вероятность «не сдать второй экзамен»: q2=1– р2=1–0,7=0,3. Оба события независимы. Вероятность события Р(А), где событие А – «студент сдаст хотя бы один экзамен», вычисляется по формуле (4.8): Р(А)=1–q1×q2 =1–0,2×0,3=1–0,06=0,94. Пример 11. Три стрелка стреляют в цель независимо друг от друга. Вероятность попадания в цель для первого стрелка равна 0,6, для второго 0,7 и для третьего 0,75. Найти вероятность:
Решение. Пусть А, В, С – события, состоящие в том, что соответственно в цель попал первый, второй, третий стрелок. Из условия задачи следует, что: Р(А) = 0,6; Р(В) = 0,7; Р(С) = 0,75. 1) Вероятность хотя бы одного попадания в цель равна: Р(А + В + С). Событие (А+В+С) – хотя бы одно попадание в цель. Вероятность хотя бы одного попадания в цель по формуле (4.8): P(A+B+C)=1- P(`A)×P(`B)×P(`C). P(A+B+C)=1– (1–0,6)×(1– 0,7)×(1– 0,75)=1– 0,4×0,3×0,25 =1-0,03= 0,97. 2) Вероятность только одного попадания в цель. Пусть D – событие, состоящее в том, что в цель попал только один стрелок. События «хотя бы одно попадание» и «одно попадание» – разные события. В задаче одно и только одно попадание – это событие D, состоящее из суммы событий: D=A×`B×`C+`A×B×`C+`A×`B×C. Его вероятность из-за независимости стрельбы и несовместности слагаемых событий может быть определена по формулам (4.2а), (4.7):
Р(D)=0,6×(1–0,7)×(1–0,75)+0,7×(1–0,6 )×(1–0,75)+0,75×(1–0,6 )×(1– 0,7) = 0,205. 3) Вероятность того, что попадут в цель только два стрелка. Пусть X – событие, состоящее в том, что в цель попали только два стрелка. X=`A×B×C+`B×A×C+`C ×A×B. Тогда вероятность того, что попадут в цель только два стрелка, равна:
P(X)=(1– 0,6)×0,7×0,75+0,6×(1– 0,7)×0,75+0,6×0,7×(1– 0,75)=0,21+0,135+0,105 =0,45. 4) Вероятность того, что попадут в цель все стрелки одновременно. Событие ABC – все стрелки попали в цель. Вероятность того, что попадут в цель все стрелки одновременно равна: P(A×B×C) = P(A)×P(B)×P(C) = 0,6×0,7×0,75 = 0,315. 5) Вероятность промаха всех стрелков одновременно Р( Событие `A×`B×`C – все промахнулись. Вероятность промаха всех стрелков одновременно: P`(A×`B×`C)=0,4×0,3×0,25=0,03. Для проверки правильности решения используют формулу (4.3) для полной группы событий: Р(D) + P(X) + P(A×B×C) + Р(`A×`B×`C) = 0,205 + 0,45 + 0,315 + 0,03 = 1.
|
||||
Вероятность полной группы событий
Множество несовместных событий образуют полную группу событий, если в результате отдельно взятого испытания обязательно появится одно из этих событий. Очевидно, что любая пара противоположных событий (в частности, примеры выше) образует полную группу. Однако в различных задачах с одним и тем же объектом могут фигурировать разные события, например, для игрального кубика характерно рассмотрение следующего набора:
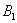 – в результате броска игрального кубика выпадет 1 очко;
– в результате броска игрального кубика выпадет 1 очко;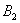 – … 2 очка;
– … 2 очка;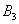 – … 3 очка;
– … 3 очка;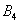 – … 4 очка;
– … 4 очка;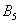 – … 5 очков;
– … 5 очков;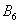 – … 6 очков.
– … 6 очков.
События 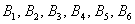 несовместны (поскольку появление какой-либо грани исключает одновременное появление других) и образуют полную группу (так как в результате испытания непременно появится одно из этих шести событий).
несовместны (поскольку появление какой-либо грани исключает одновременное появление других) и образуют полную группу (так как в результате испытания непременно появится одно из этих шести событий).
Противоположные события
Два события называются совместными, если появление одного из них не исключает появление другого в одном и том же испытании.
Два события называются противоположными, если в данном испытании они несовместны и одно из них обязательно происходит. Вероятности противоположных событий в сумме дают 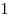 .
.
Если событие  может произойти с вероятностью
может произойти с вероятностью  и опыт повторяют
и опыт повторяют  раз, то вероятность, что оно наступит хотя бы один раз, есть:
раз, то вероятность, что оно наступит хотя бы один раз, есть: 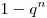 , где
, где 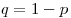 .
.


 ,
,
 .
. .
. ).
).