Теорема сложения вероятностей

Версия 1: Формулировка теоремы сложения вероятностей

Теорема

Вероятность суммы двух несовместимых событий равна сумме вероятностей этих событий.

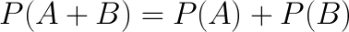
Несколько событий называются несовместными, если никакие из них не могут появиться одновременно в результате однократного испытания случайного эксперимента.

Теорема сложения вероятностей применима к любому числу несовместных событий:

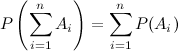
Говорят, что события 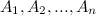образуют полную группу событий, если в результате опыта обязательно произойдет, хотя бы одно из событий этой группы.

Следствие 1. Если события 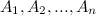образуют полную группу несовместных событий, то сумма их вероятностей равна единице:

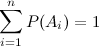
Противоположными событиями называются два несовместных события, образующих полную группу.

Следствие 2. Сумма вероятностей противоположных событий равна единице:

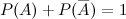
здесь 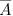- событие, противоположное событию .

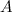Версия 2:

Теорема. Вероятность суммы конечного числа несовместных событий $A_1, A_2,...A_n$ равна сумме вероятностей этих событий

(2.1)

Доказательство. Докажем эту теорему для случая суммы двух несовместных событий $A_1$ и $A_2$ .

Пусть событию $A_1$ благоприятствуют $m_1$ элементарных исходов, а событию $A_2 - m_2$ исходов. Так как события $A_1$ и $A_2$ по условию теоремы несовместны, то событию $A_1+ A_2$ благоприятствуют $m_1 + m_2$ элементарных исходов из общего числа n исходов. Следовательно,

где $P(A_1)$ — вероятность события $A$ ; $P(A_2)$ — вероятность события $A_2$ .

Пример. Для отправки груза со склада может быть выделена одна из двух машин различного вида. Известны вероятности выделения каждой машины: $P(A_1)=0,2, P(A_2)=0,4$ . Тогда вероятность поступления к складу хотя бы одной из этих машин будет

P(А₁+А₂) = 0,2 + 0,4 = 0,6.

Условная вероятность

Во многих случаях вероятности появления одних событий зависят от того, произошло или нет другое событие. Например, вероятность своевременного выпуска машины зависит от поставки комплектующих изделий. Если эти изделия уже поставлены, то искомая вероятность будет одна. Если же она определяется до поставки комплектующих, то ее значение, очевидно, будет другим.

Вероятность события $A$ , вычисленная при условии, что имело место другое событие $B$ , называется условной вероятностью события $A$ и обозначается $P(A/B)$ .

В тех случаях, когда вероятность события $A$ рассматривается при условии, что произошло два других события $(B, C)$ , используется условная вероятность относительно произведения событий $(B, C)$

$P(A/BC)$ .

Теорема сложения вероятностей совместных событий

Два события называются совместными, если появление одного из них не исключает появления другого в одном и том же опыте.

Пример. Поступление в магазин одного вида товара — событие $A$ . Поступление второго вида товара — событие $B$ . Поступить эти товары могут и одновременно. Поэтому $A$ и $B$ - совместные события.

Теорема. Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления

P(A+B) = P(A) + P(B) — P(AB). (2.5)

Доказательство. Событие $A+B$ наступит, если наступит одно из трех несовместных событий $A \overline{B}$ , $\overline{A}B$ , $AB$ . По теореме сложения вероятностей несовместных событий имеем

(2.6)

Событие $A$ произойдет, если наступит одно из двух несовместных событий: $A\overline{B}$ , $AB$ . Вновь применяя теорему сложения вероятностей несовместных событий, получаем $P(A) = P(A \overline{B} ) + P(AB)$ . Откуда

(2.7)

Аналогично для события Откуда

.(2.8)

Подставив (2.7) и (2.8) в (2.6), находим

P(A+B) = P(A) + P(B) — P(AB).

Пример. Если вероятность поступления в магазин одного вида товара равна P(A) = 0,4, а второго товара — P(B) = 0,5, и если допустить, что эти события независимы, но совместны, то вероятность суммы событий равна

P(A+B) = 0,4 + 0,5 — 0,4×0,5 = 0,7.