Относительной частотой события называют отношение числа испытаний, в которых событие появилось (m), к общему числу фактически произведённых испытаний (n).
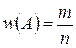
Итак, классическое определение вероятности не требует, чтобы испытания производились в действительности; статистическое определение вероятности - определение относительной частоты предполагает, что испытания были произведены фактически. Другими словами, классическую вероятность вычисляют до опыта, а статистическую вероятность или относительную частоту – после опыта.
Свойство устойчивости: В различных опытах относительная частота изменяется мало (тем меньше, чем больше произведено испытаний), колеблясь около некоторого постоянного числа (вероятности события).
По статистике частота рождения мальчика – 0,51; а девочки – 0,49; согласно классическому определению вероятности вероятность рождения мальчика равна вероятности рождения девочки – 0,5.
Устойчивость относительной частоты.
события A, (
— число проведенных испытаний, 
— число испытаний, в которых наступило событие A) обладает свойством статистической устойчивости, то есть при большом числе испытаний её значение стремится к одному и тому же числу. Это число есть вероятность появления события A.Классическое определение вероятности. Пусть испытание сводится к схеме случаев (исходы образуют полную группу событий и равновозможны, т.е. единственно возможны, несовместны и равновозможны), тогда вероятность события А равно отношению числа случаев, благоприятствующих событию А к общему числу случаев:
P(A)=
=
.
Классическое определение вероятности долгое время рассматривалась как определение вероятности (с 17 по 19 века), т.к. в то время методы теории вероятности применялись к азартным играм и сводились к схеме случаев.
Из классического определения вероятности вытекают следующие свойства:
-
Т.к. 0
m
n, то 0
1. -
Пусть А – достоверное событие, тогда m=n, то P(Ω)=1.
-
Пусть А – невозможное событие, тогда m=0, то P(
)=0.
Статистическое определение вероятности. Если исходы не равновозможны или число исходов испытания бесконечно, то классическое определение вероятности нельзя использовать.
Есть совершенно новый подход к определению вероятности событий, основывающийся на том, насколько часто будет проявляться данное событие в последовательности проведённых испытаний. В данном случае используется статистическое определение вероятности.
Статистической вероятностью события А называется относительная частота появления этого события M в N произведённых испытаниях:
(А)=
.
Для получения более точного результата необходимо увеличить число испытаний.
Геометрическое определение вероятности
Чтобы преодолеть недостаток классического определения вероятности, состоящий в том, что оно неприменимо к испытаниям с бесконечным числом исходов, вводят геометрические вероятности ? вероятность попадания точки в область (отрезок, часть плоскости и т.д.).
Пусть отрезок l составляет часть отрезка L. На отрезок L на удачу поставлена точка. Это означает выполнение следующих предположений: поставленная точка может оказаться в любой точке отрезка L, вероятность попадания точки на отрезок l пропорциональна длине этого отрезка и не зависит от его расположения относительно отрезка L. В этих предположениях вероятность попадания точки на отрезок l определяется равенством. P = Длина l / длина L.
Пусть плоская фигура g составляет часть плоской фигуры G. На фигуру G на удачу брошена точка. Это означает выполнение следующих предположений: брошенная точка может оказаться в любой точке фигуры G, вероятность попадания брошенной точки на фигуру g пропорциональна площади этой фигуры и не зависит от его расположения относительно фигуры G, ни от формы g. В этих предположениях вероятность попадания точки на фигуру g определяется равенством. P = Площадь g / Площадь G.
